梯度下降
梯度下降是很常用的算法,它不仅被用在线性回归上和线性回归模型、平方误差代价函数
通过不断调整θi 的大小来不断使代价函数最小

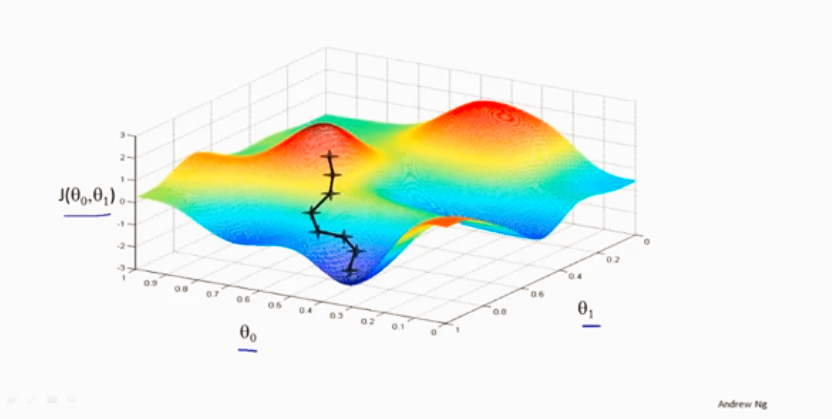
梯度下降的算法
同时更新参数

导数项的含义
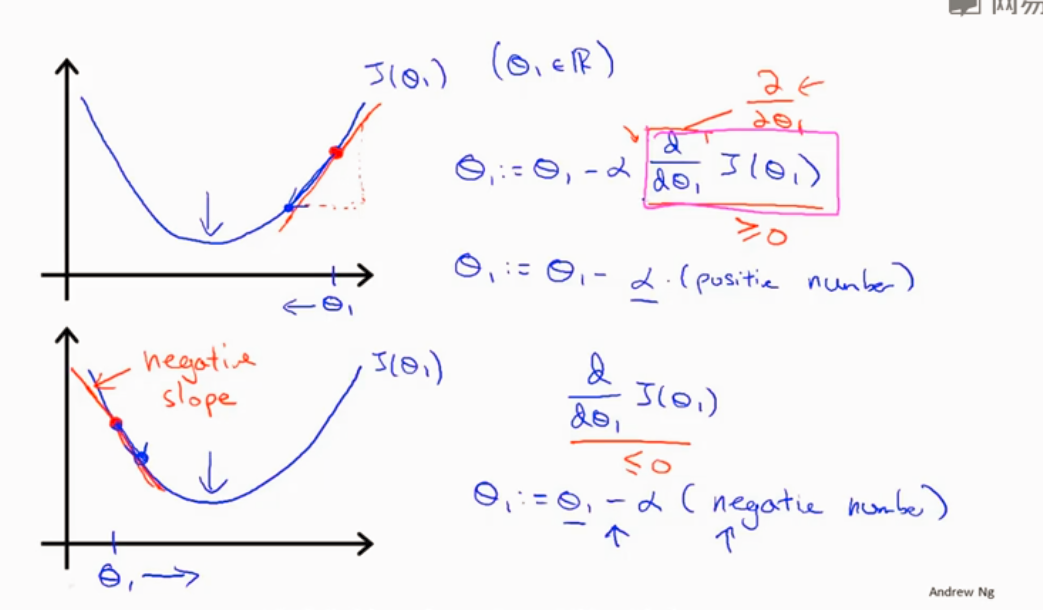
α 学习速率 太大或者太小的情况如下图
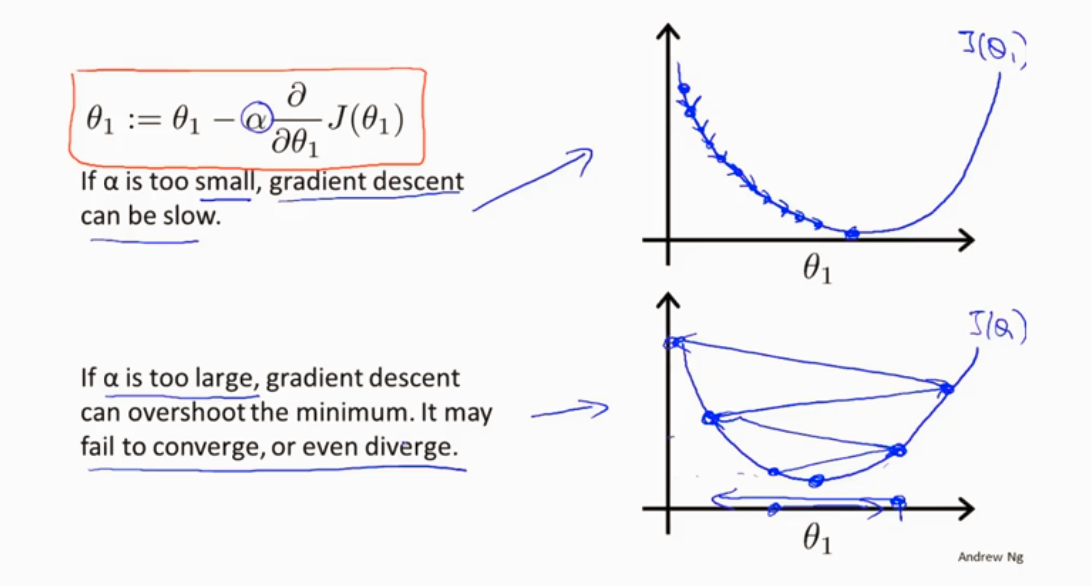
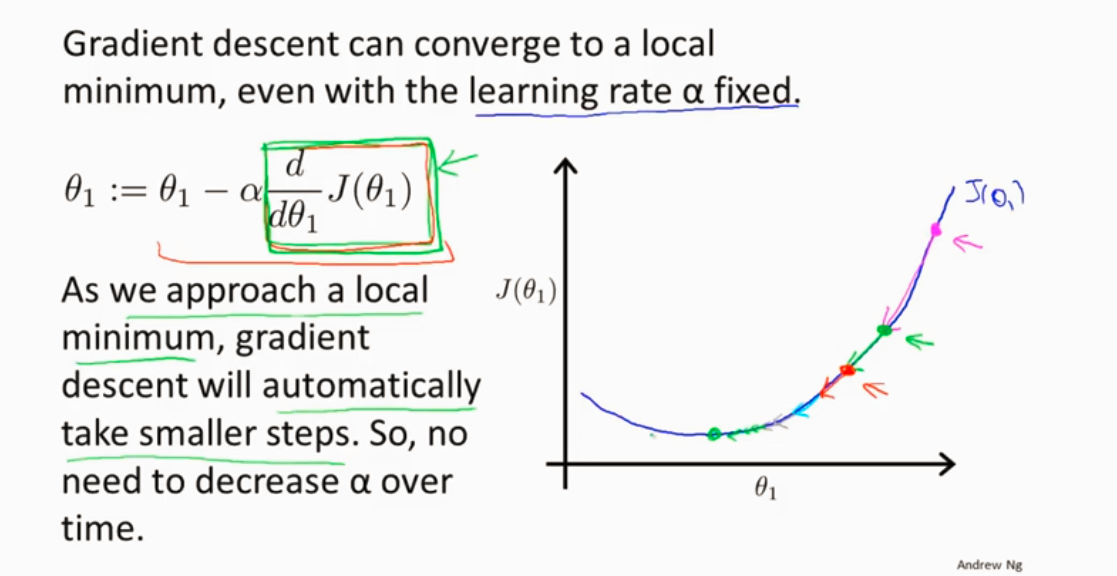
局部最优 导数为0,θ不变了
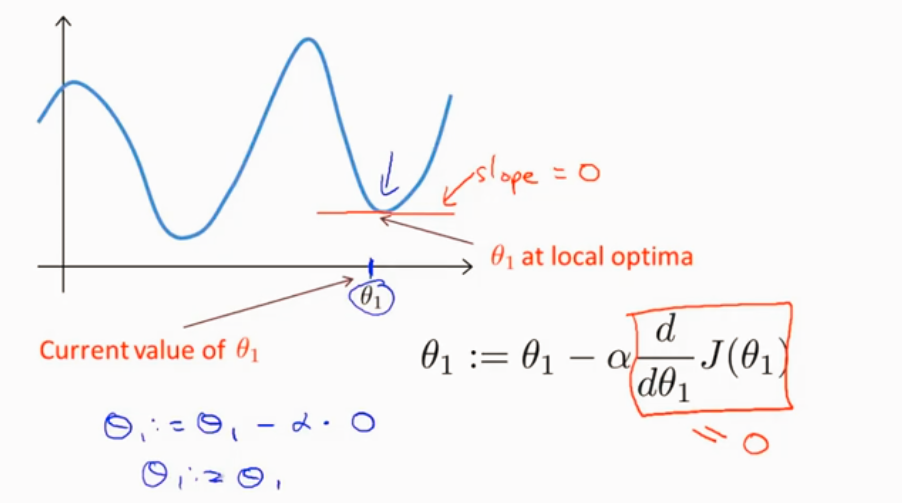
越接近局部最优点,梯度下降自动选取小幅下降,因为越接近局部最优,导数越来越小。
代价函数
什么是代价函数?
假设有训练样本(x, y),模型为h,参数为θ。h(θ) = θTx(θT表示θ的转置)。
(1)概况来讲,任何能够衡量模型预测出来的值h(θ)与真实值y之间的差异的函数都可以叫做代价函数C(θ),如果有多个样本,则可以将所有代价函数的取值求均值,记做J(θ)。因此很容易就可以得出以下关于代价函数的性质:
- 对于每种算法来说,代价函数不是唯一的;
- 代价函数是参数θ的函数;
- 总的代价函数J(θ)可以用来评价模型的好坏,代价函数越小说明模型和参数越符合训练样本(x, y);
- J(θ)是一个标量;
代价函数的常见形式
均方误差
在线性回归中,最常用的是均方误差(Mean squared error),具体形式为:
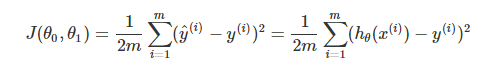
m:训练样本的个数;
hθ(x):用参数θ和x预测出来的y值;
y:原训练样本中的y值,也就是标准答案
上角标(i):第i个样本
线性回归的代价函数3D图
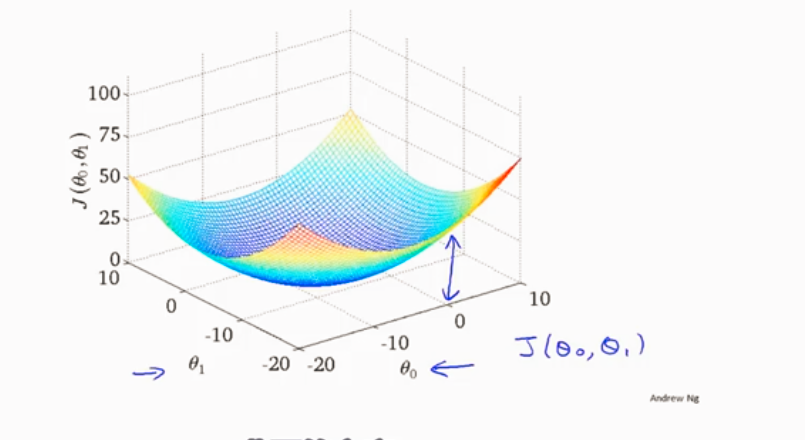
梯度下降和代价函数结合 得到线性回归算法

下面看看对J求偏导的步骤
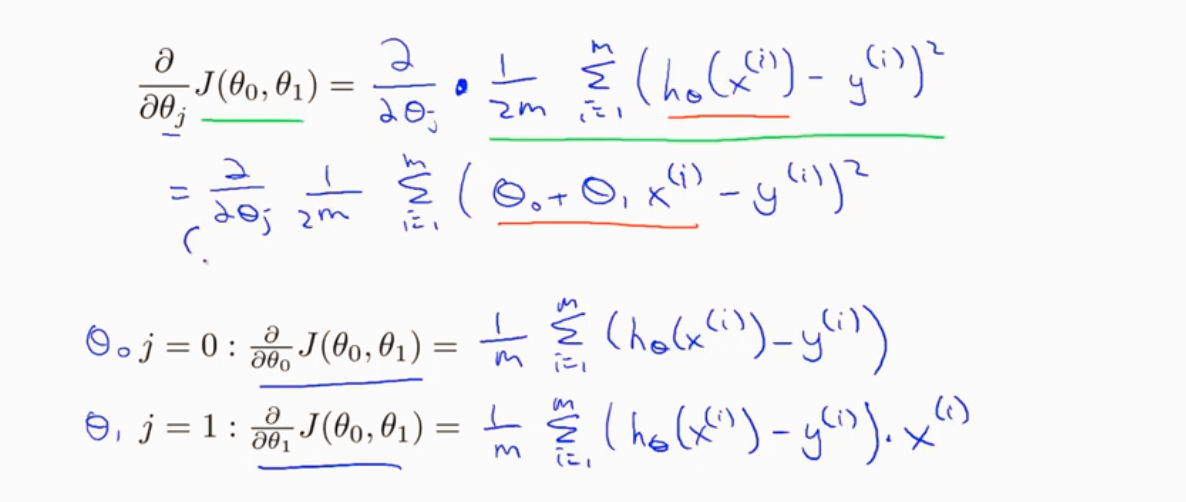

凸函数 没有局部最优只有全局最优
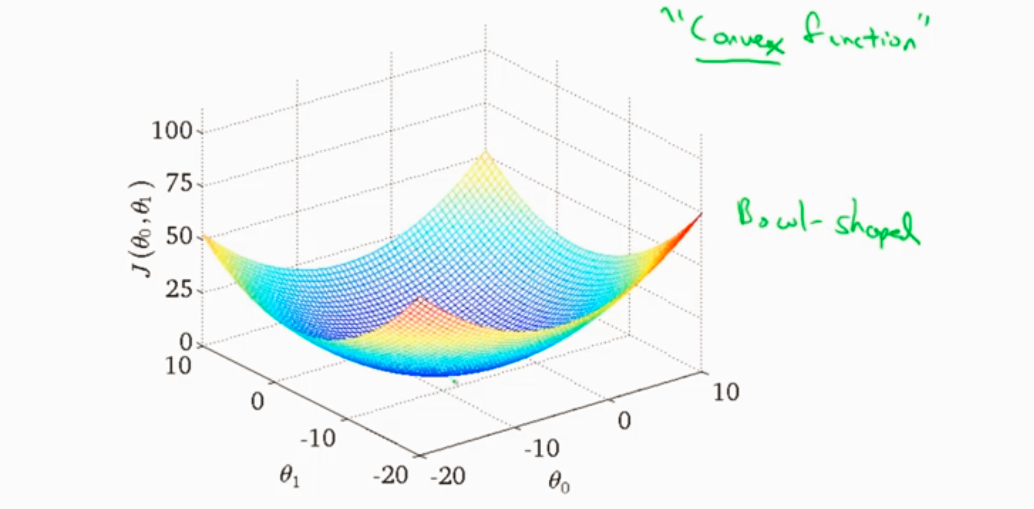
批量梯度下降:用到了所有数据集
正则化和过拟合问题
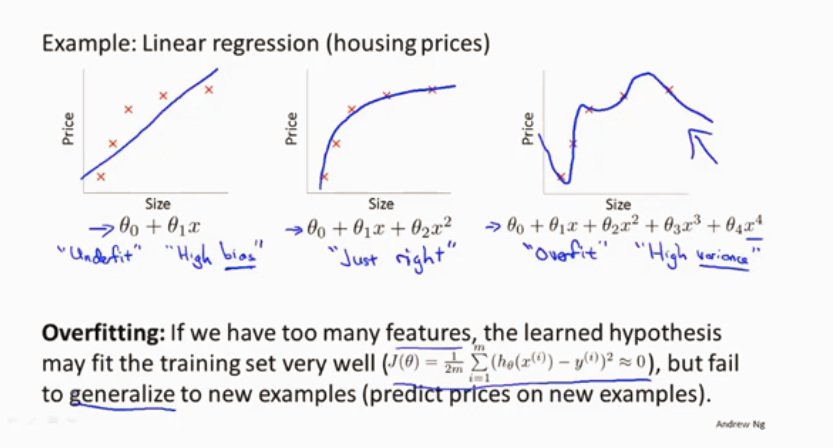
过拟合不能很好地泛化(应用预测在新样本)
线性回归的欠拟合和过拟合
逻辑回归的欠拟合和过拟合
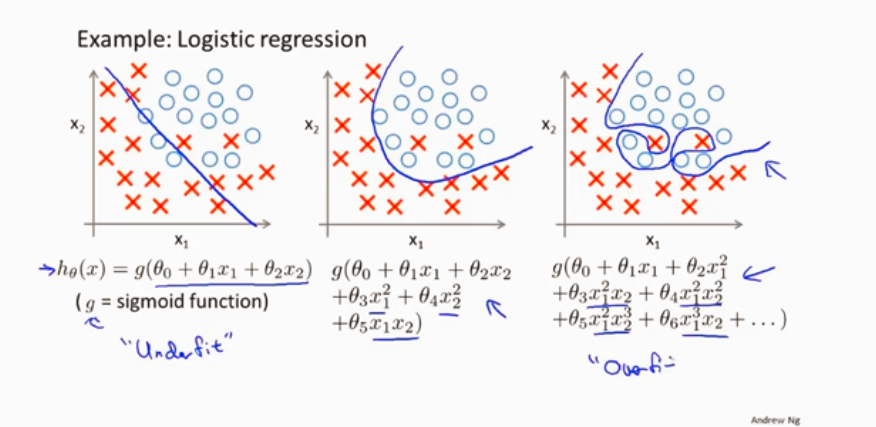
解决过拟合的方法
1、减少选取变量的数量(缺点就是舍弃变量会舍弃掉一些信息) 可以是手工选择保留哪些特征,或者使用一些模型选择的算法来帮忙(例如PCA)
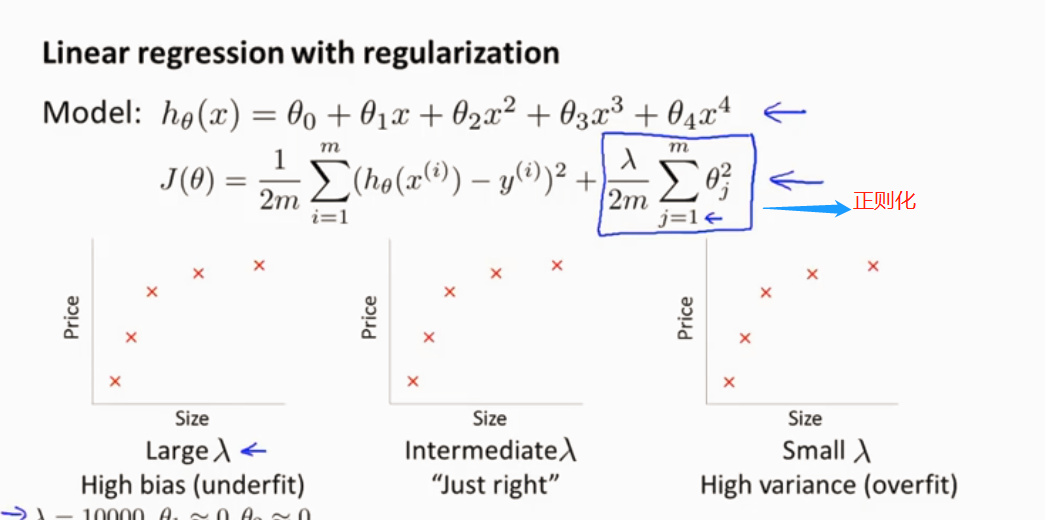
2、正则化 保留所有的特征,但是减少参数的大小(magnitude)。

通过是后两项参数接近于0 来使其发挥不了太大作用
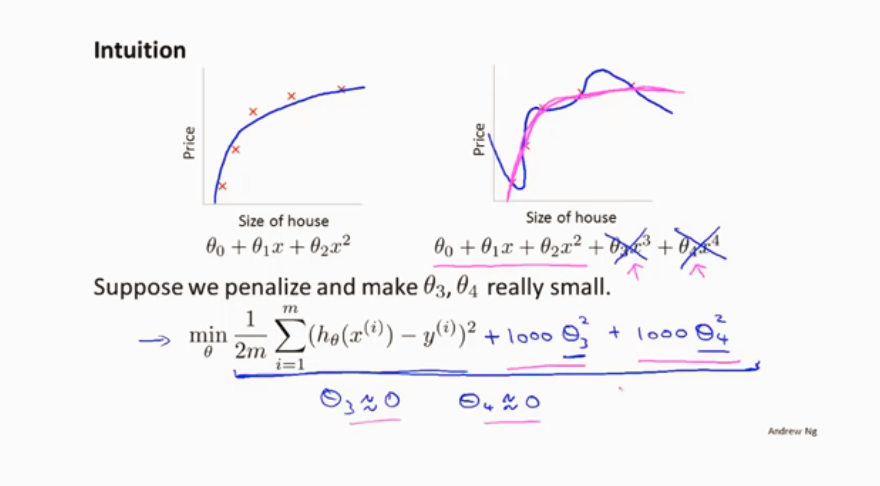
缩小每一个参数 来使其变的平缓,不容易出现过拟合

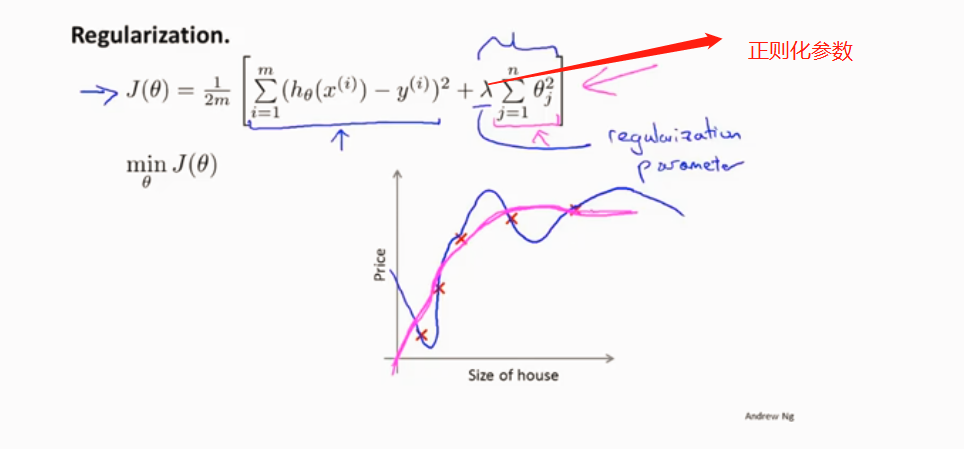
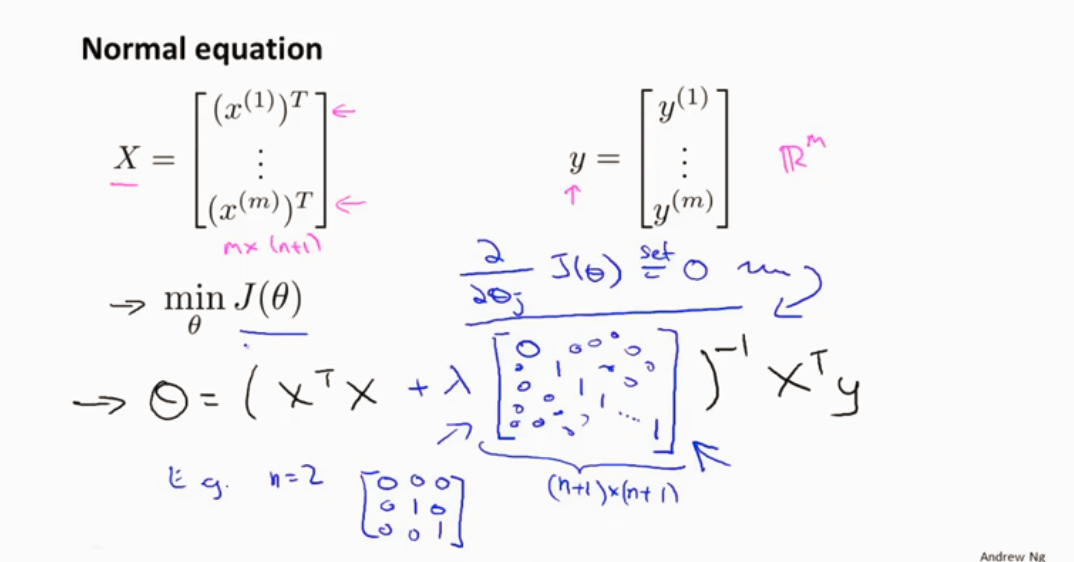
线性回归的正则化

梯度下降 加上正则化项

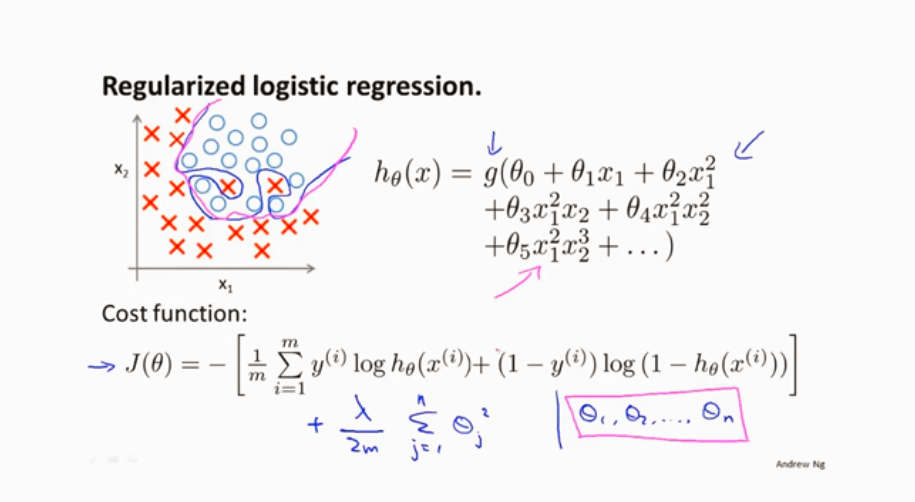
逻辑回归的正则化
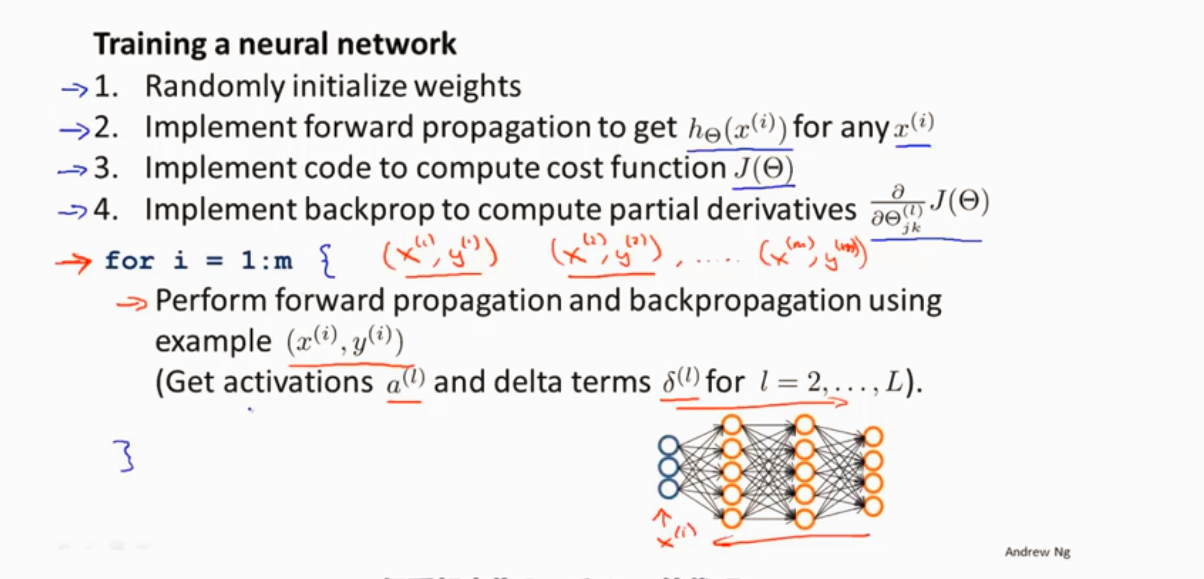
训练神经网络步骤
1、随机初始化权值为接近0的
2、前向传播
3、通过代码代价函数J()
4、反向传播计算偏导数项
5、梯度检验 梯度下降

数据集分三类 训练集、测试集、验证集。 比例为 60%:20%:20%
测试数据随机选择比较好
过拟合欠拟合 偏差 方差
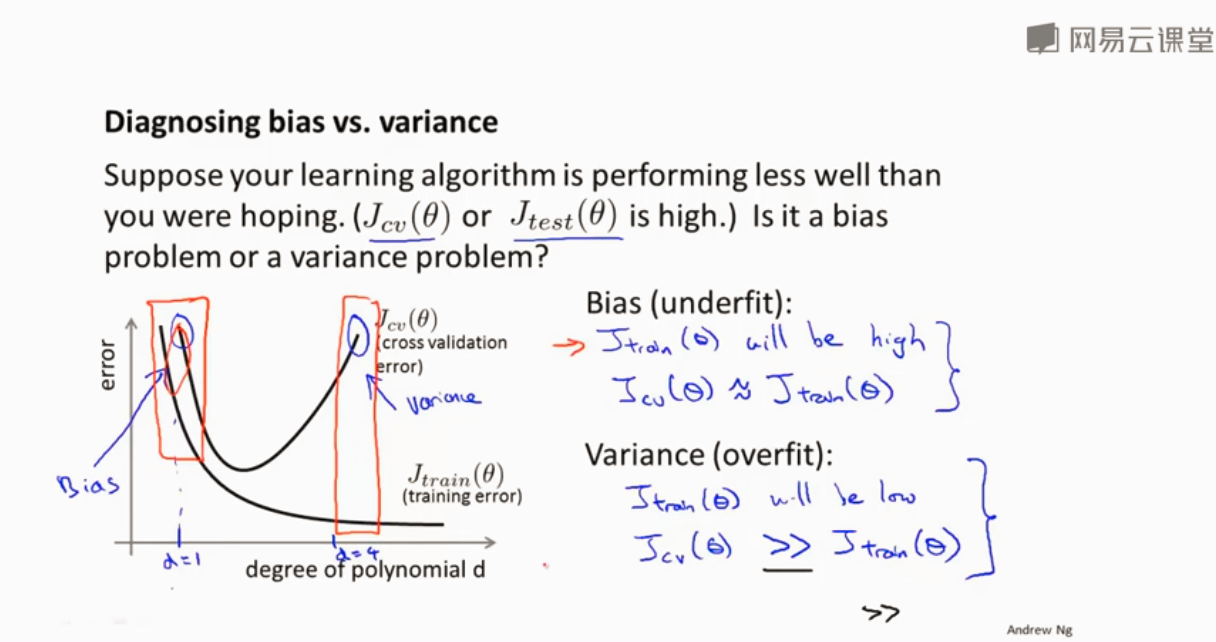
为了防止过拟合 正则化
训练和验证误差定义不包括正则化项
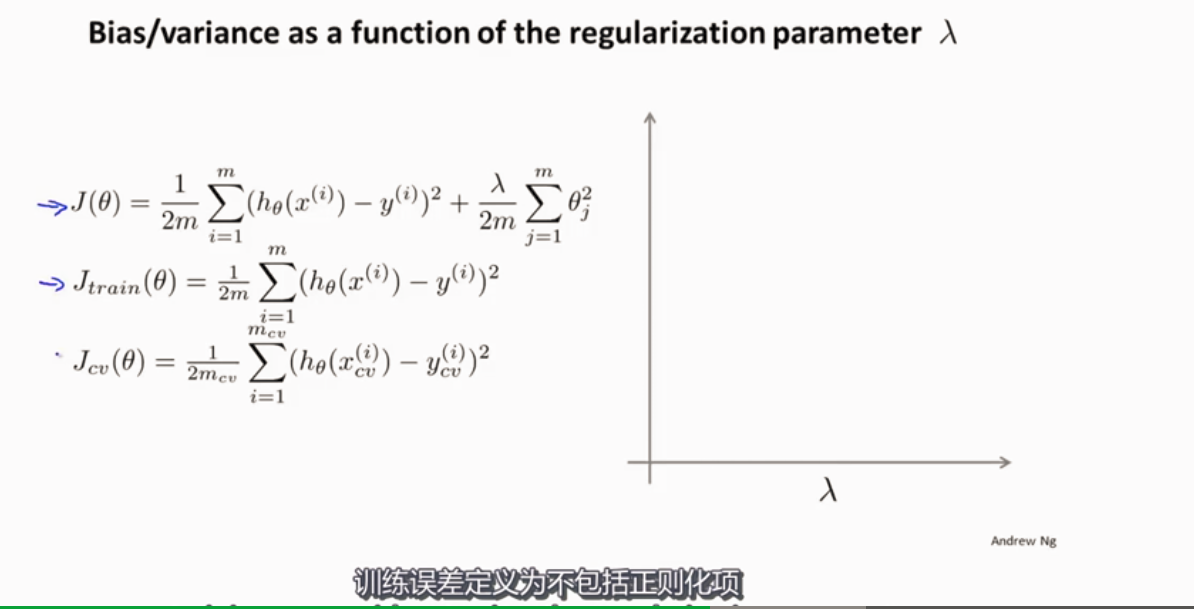
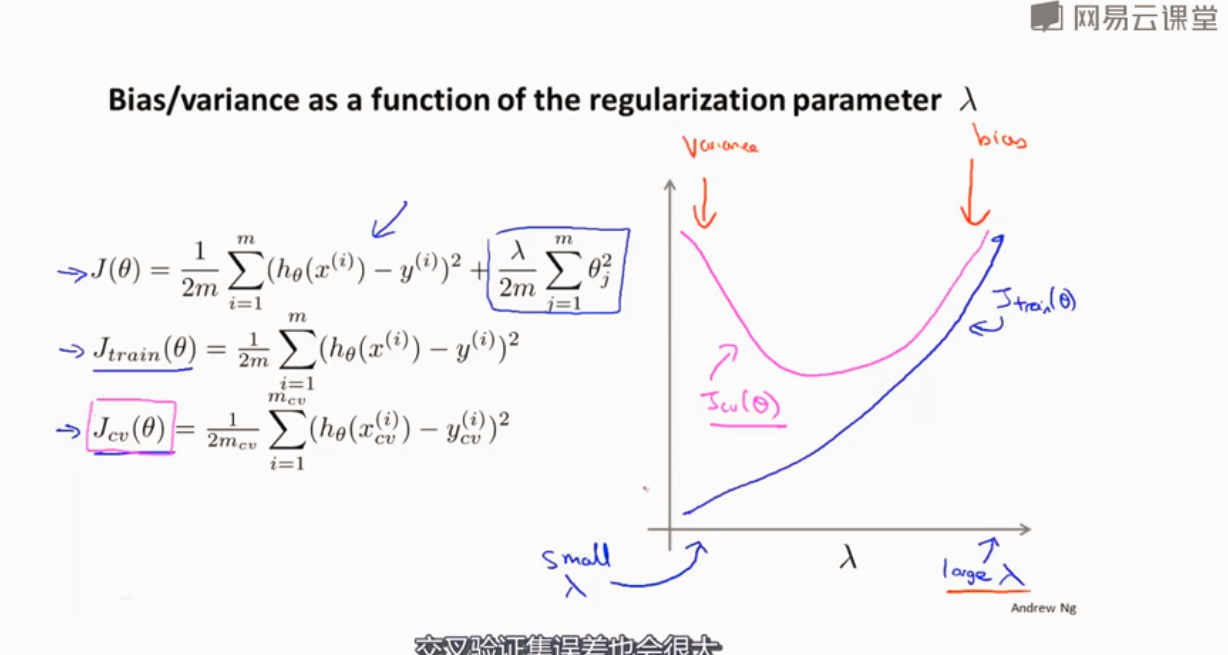
选取合适的λ
学习曲线来判断算法与改进算法
当选二次函数时,训练误差随着训练样本的增加而增加,而交叉验证误差随之减小
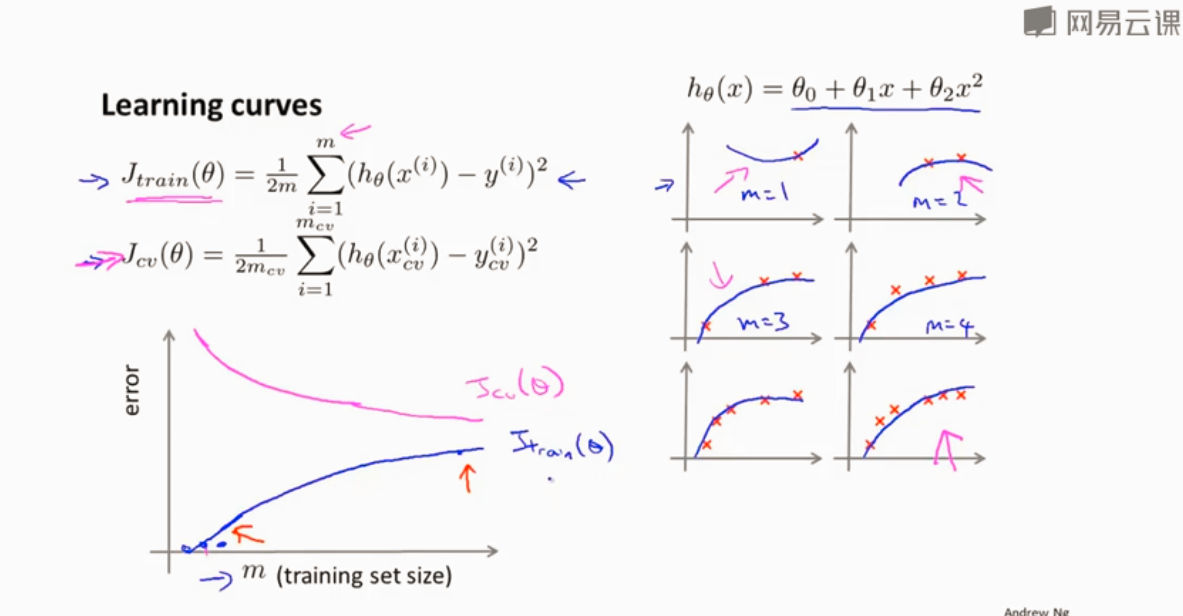
处于高偏差
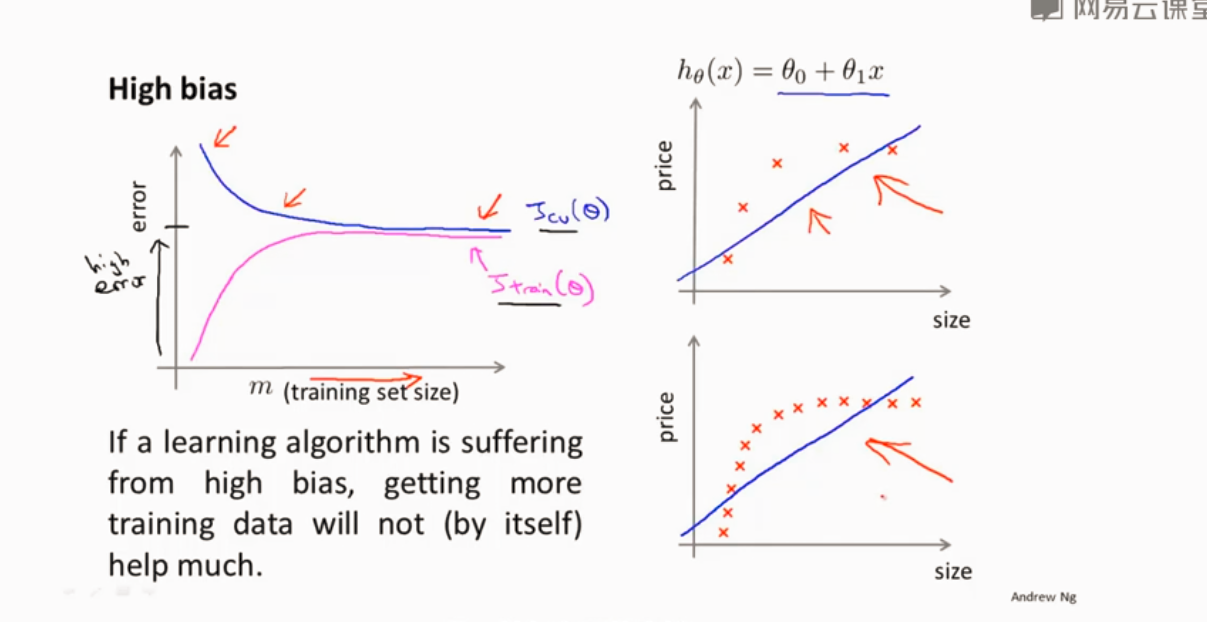
高方差
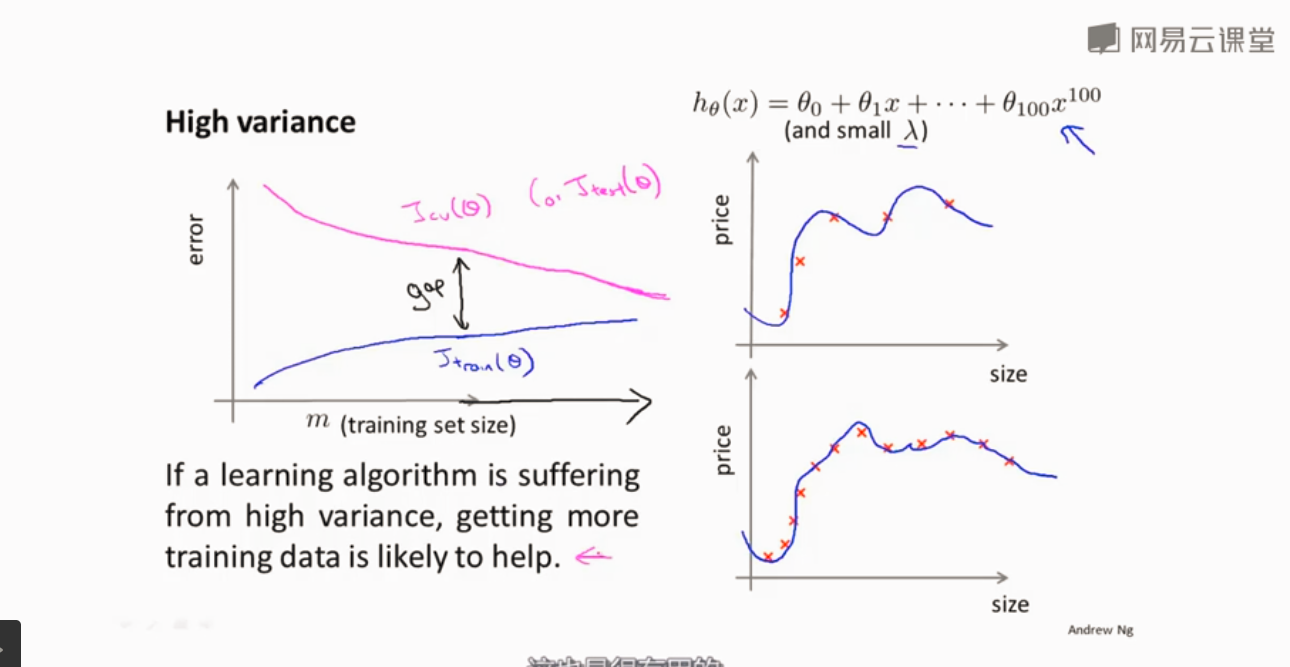
高方差选取一些部分特征 减小λ
高偏差 增加特征 增加λ

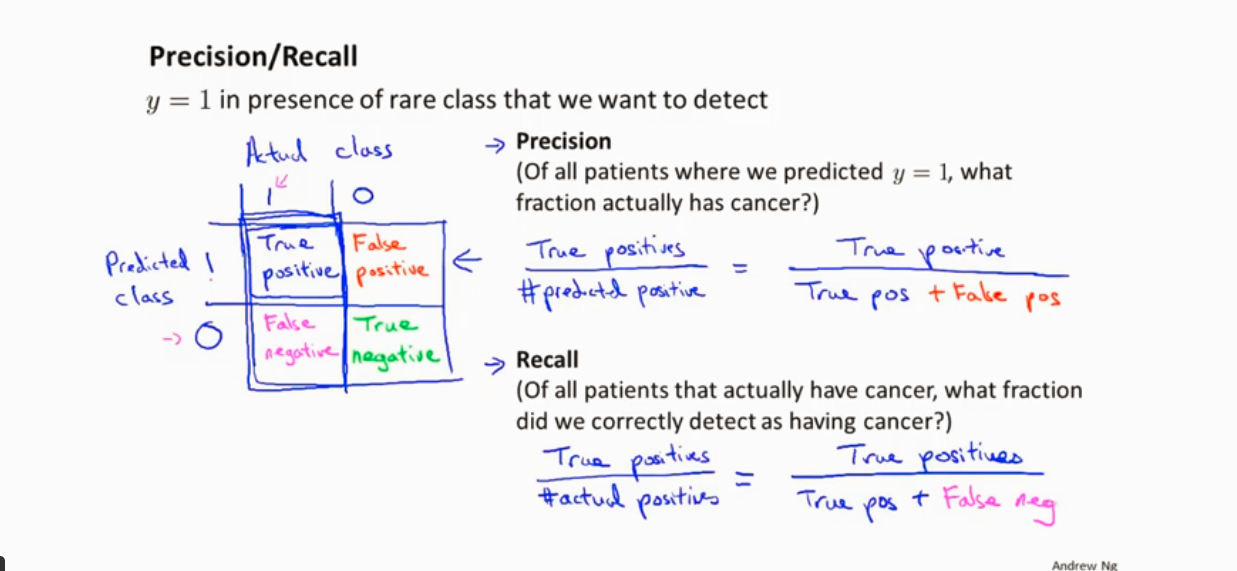
查准率和召回率 (针对偏斜类的情况下使用较好)
以得癌症的例子为例
查准率: 实际为 positive 的 / 预测 为 positive 的 越高越好
召回率: 预测为 positice的 / 实际上为 positice的 越高越好
支持向量机(SVM)
先看看逻辑回归 激活函数 如下
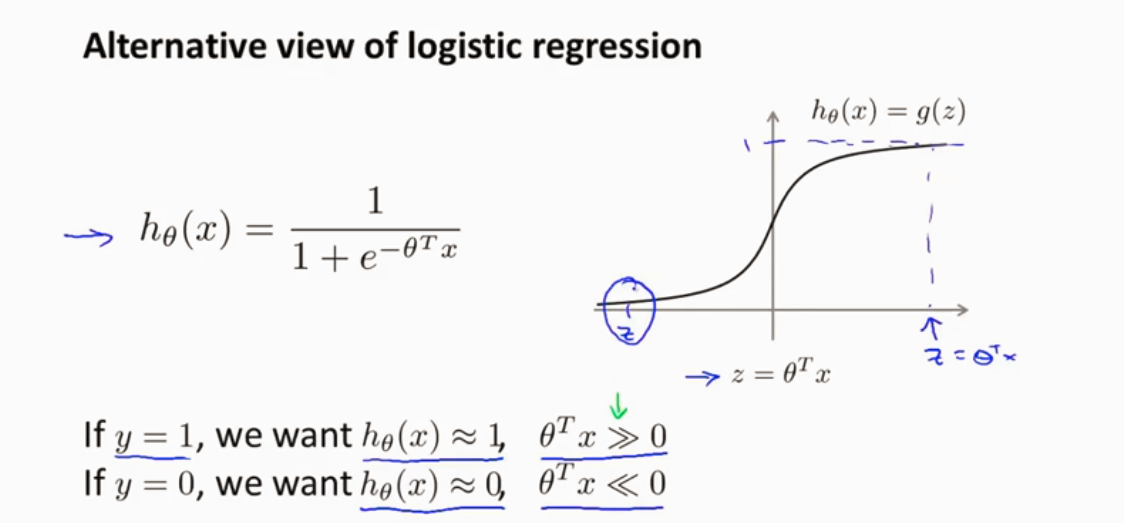
逻辑回归代价函数: 先看看每个样本对代价函数的,在求样本求和
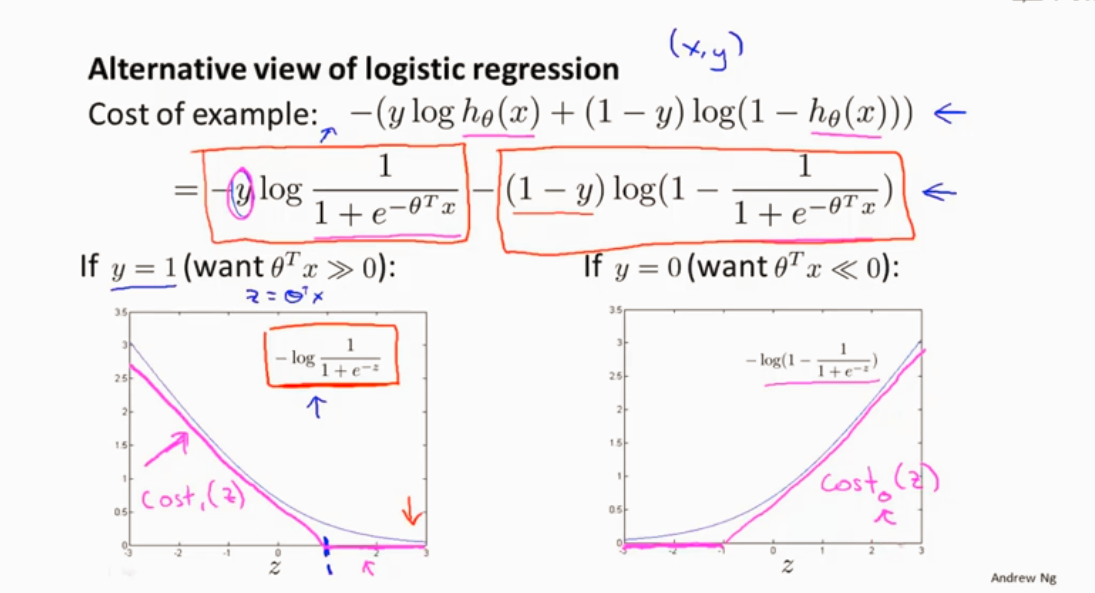
逻辑回归的代价函数J
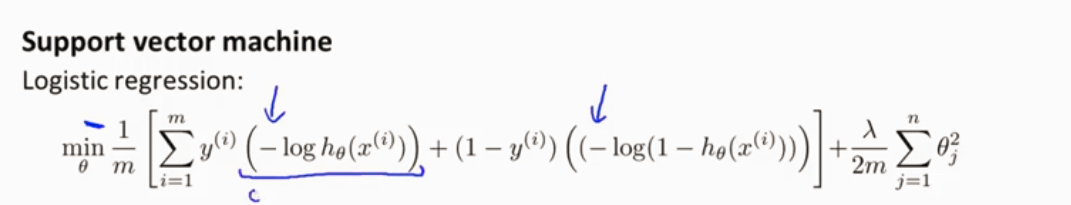
SVM算法步骤
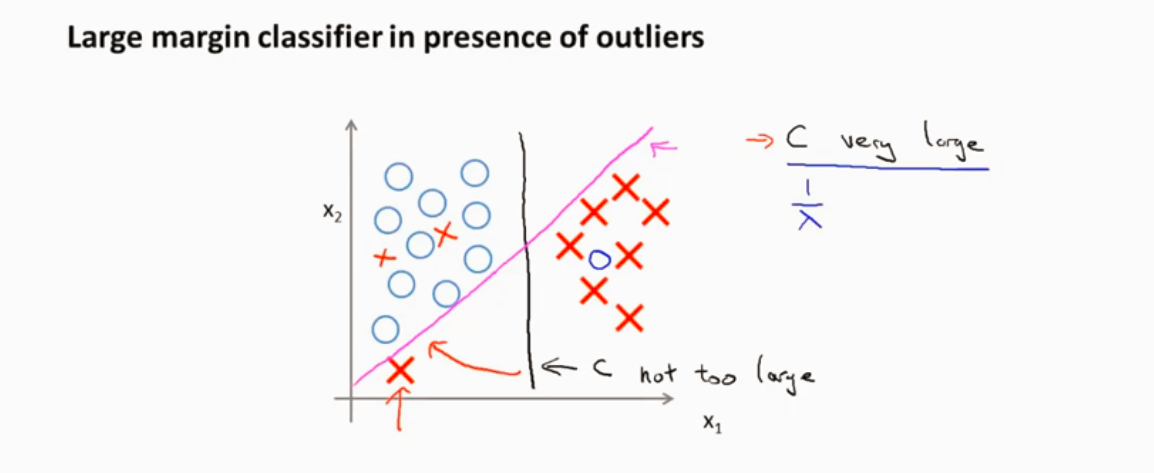
首先消去1/m,之后逻辑回归代价函数项前一部分设为A,正则化项设为B,如下图。

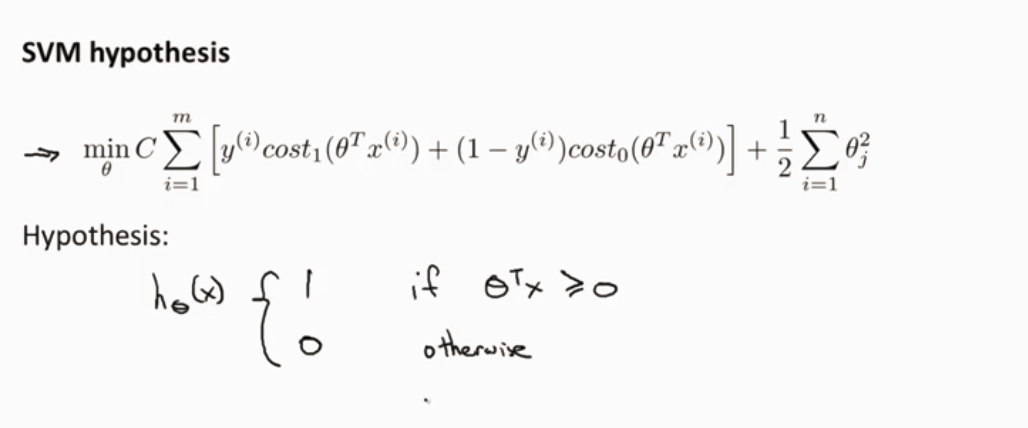
SVM y=1 和 y=0

假设C很大,
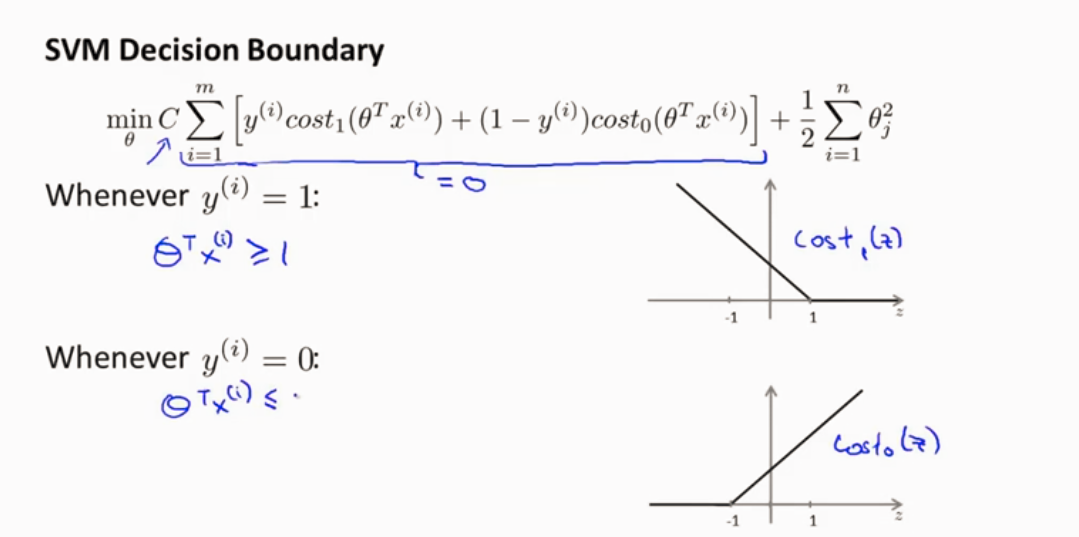
SVM 选择最大间隔 因此SVM也叫最大间隔分类器
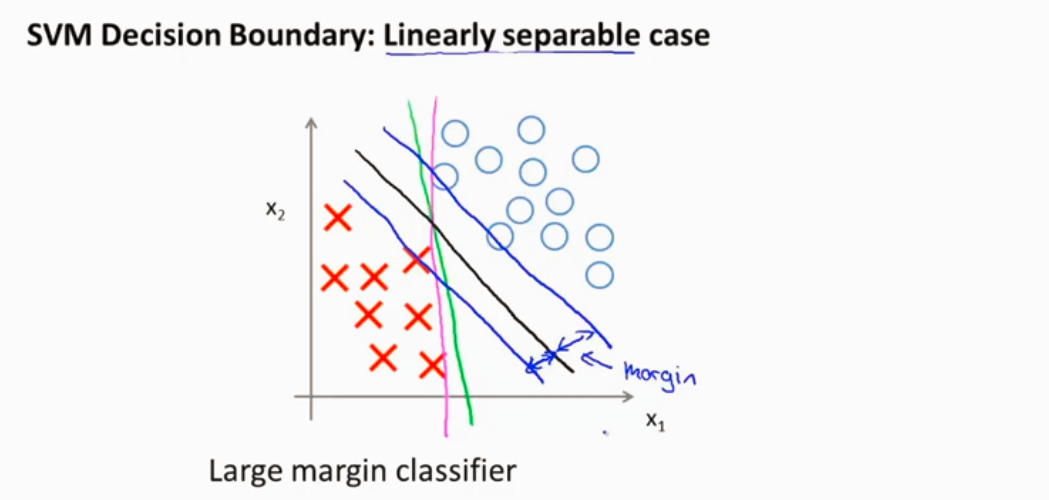
当C很大的时候 会因为一些异常点而改变最大间隔分类 不是很好
SVM为什么选择最大间隔推导
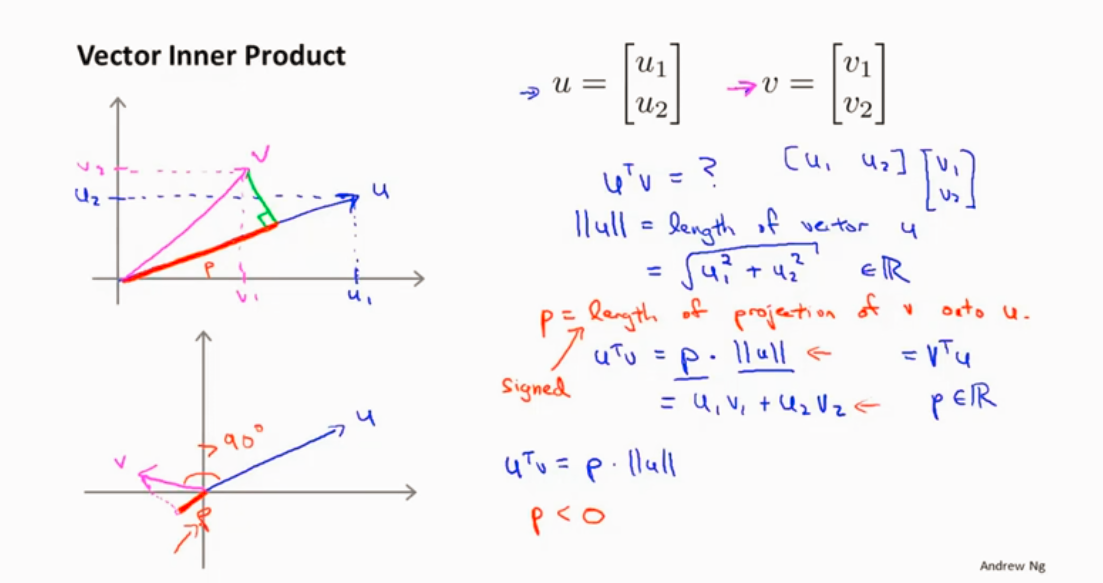
向量内积
优化目标函数
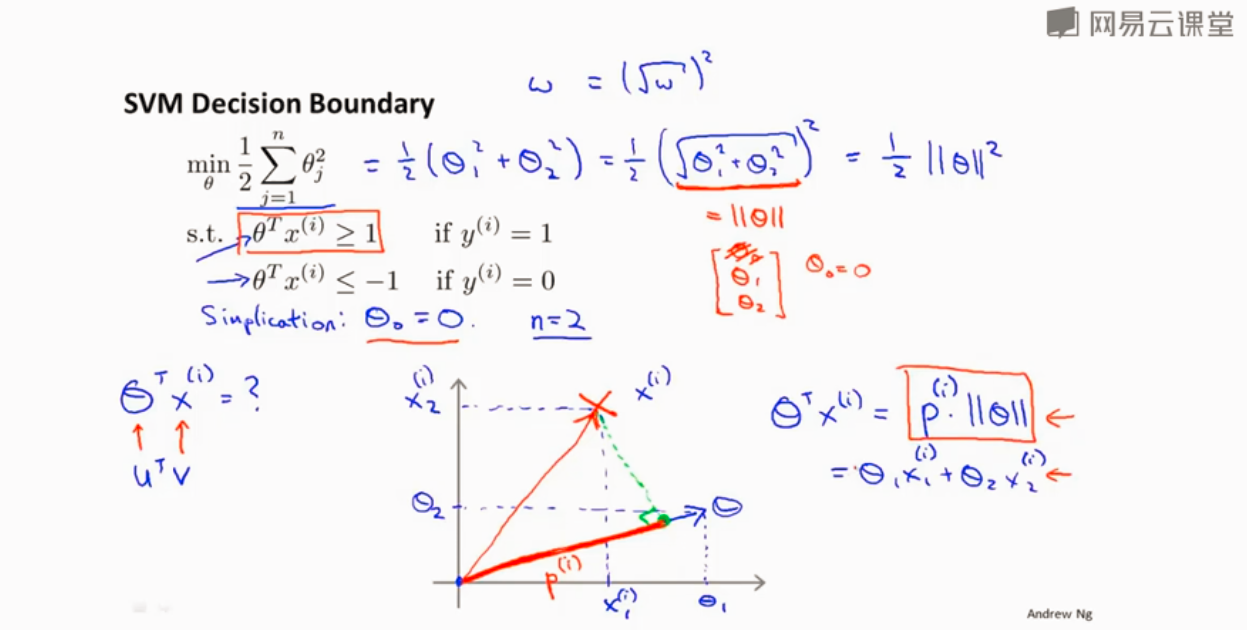
对于这样选择的参数θ ,可以看到参数向量 事实上是和决策界是90度正交的。SVM之所以最大间隔分类是因为想最大P,所以就是训练样本到决策边界距离大。
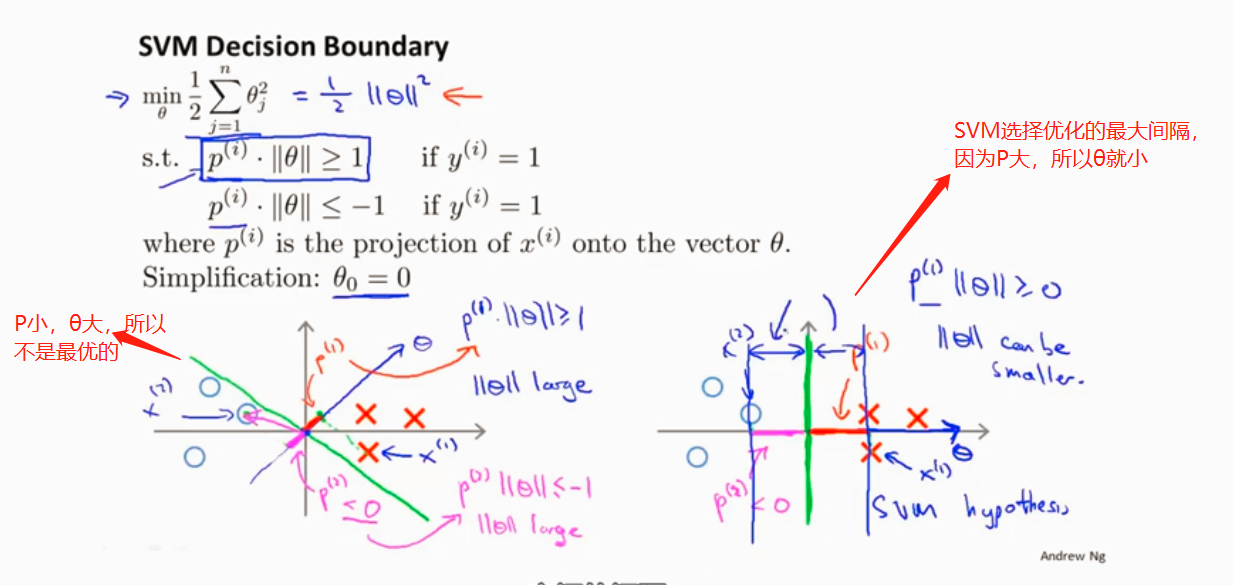
SVM核函数
高斯核函数
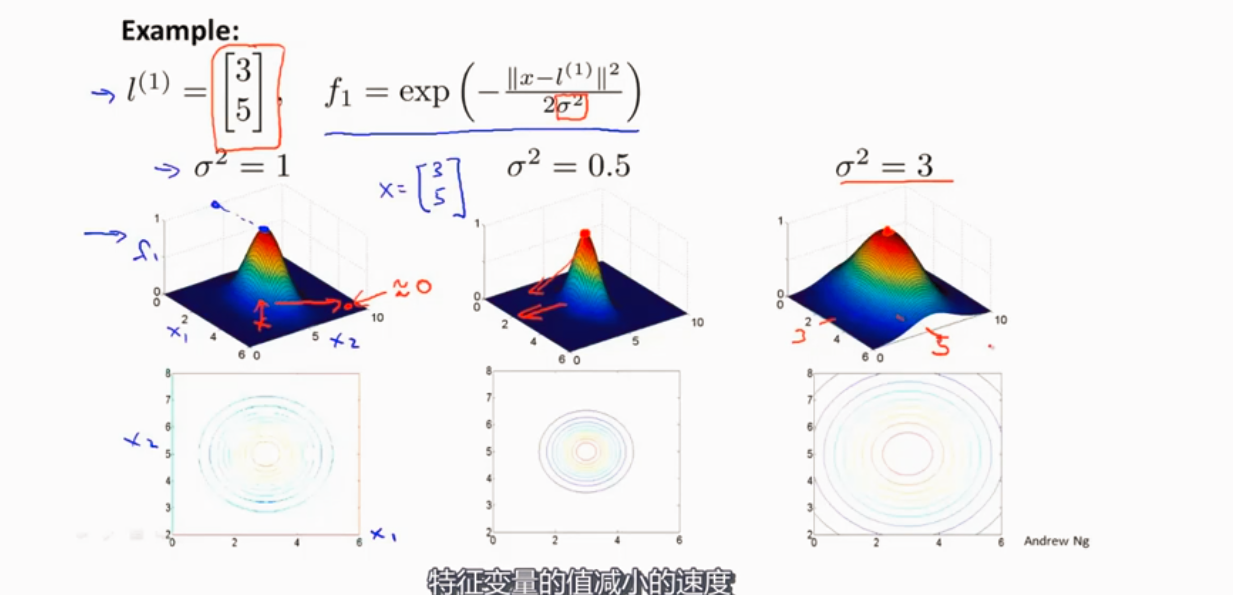


使用SVM
线性核函数和高斯核函数 两个常用的核函数

样本特征n多,但是训练数据m少,用线性核函数
n小,m大小适中,,高斯核函数
n小,m大 高斯核函数运行很慢,创建更多的特征,用逻辑回归或者不用核函数(即线性核函数)

神经网络比SVM包慢 SVM优化的问题是凸优化问题 SVM不用担心局部最优。神经网络则需要考虑局部最优问题。
逻辑回归

该函数的图像为:
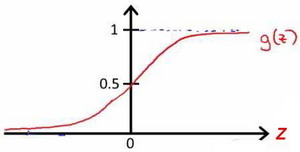

无监督学习
聚类算法
K-Means算法
K-Means算法是迭代算法
1、簇分配
遍历每一个样本点,找到 离哪个簇中心近的,并将其分类
2、移动聚类中心
找出所有一个簇的均值 然后把簇中心移动到那一类
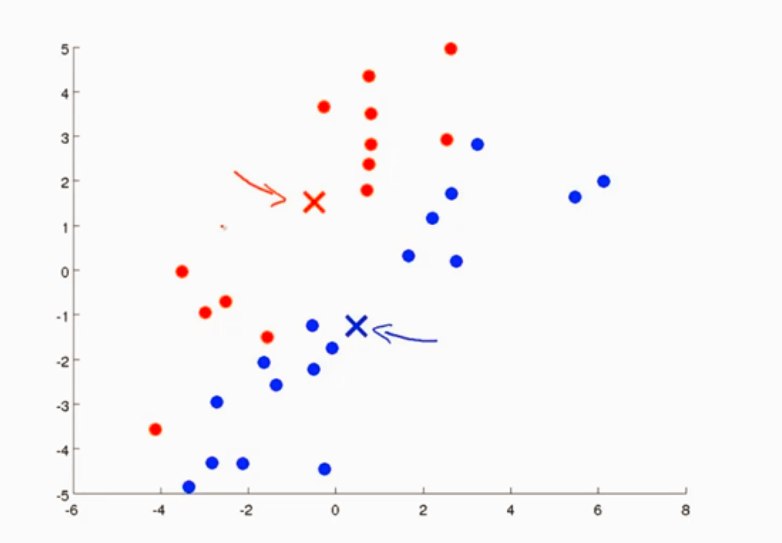
样本点变了所以再次移动聚类中心
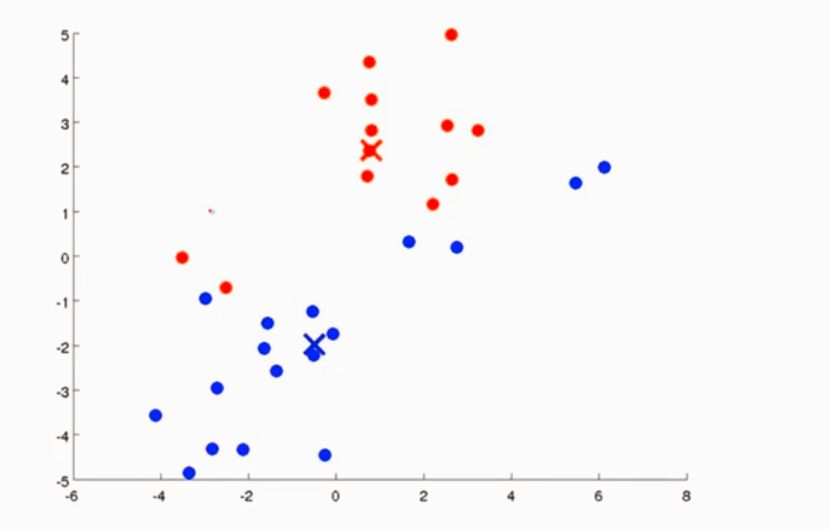
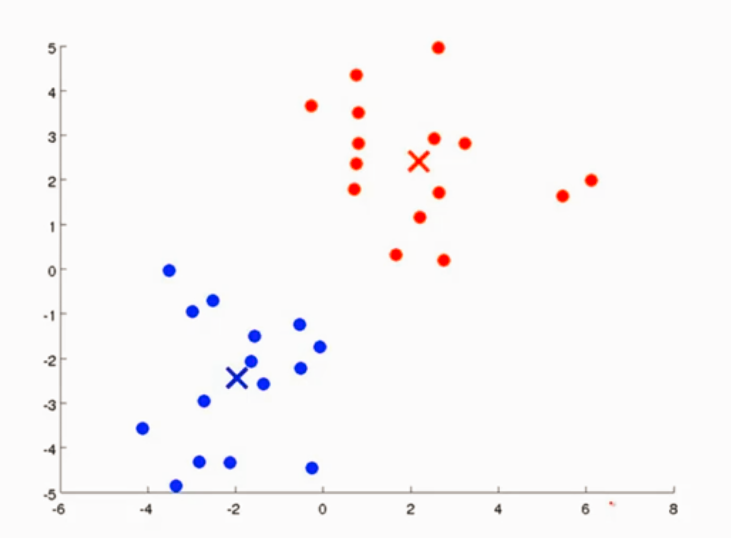
K-Means接受两个参数 一个是K 簇的数量 另一个参数是X表示的训练集 n维

1.随机初始化
2.循环 对每个样本看它离哪一个簇的聚类中心更近 便将其染成相同颜色
或者 遍历每一个聚类中心,看这个点离哪一个聚类中心更近
3.移动聚类中心 算出这个簇的均值 然后移动聚类中心
如果有一次簇没有样本,则可以直接移除这个簇聚类中心 这是通常做法,这样簇的数量就会变成K-1,如果需要K个簇的话可以重新随机初始化聚类中心。

优化目标函数

K-means算法步骤

如何随机初始化聚类中心
随机选样本
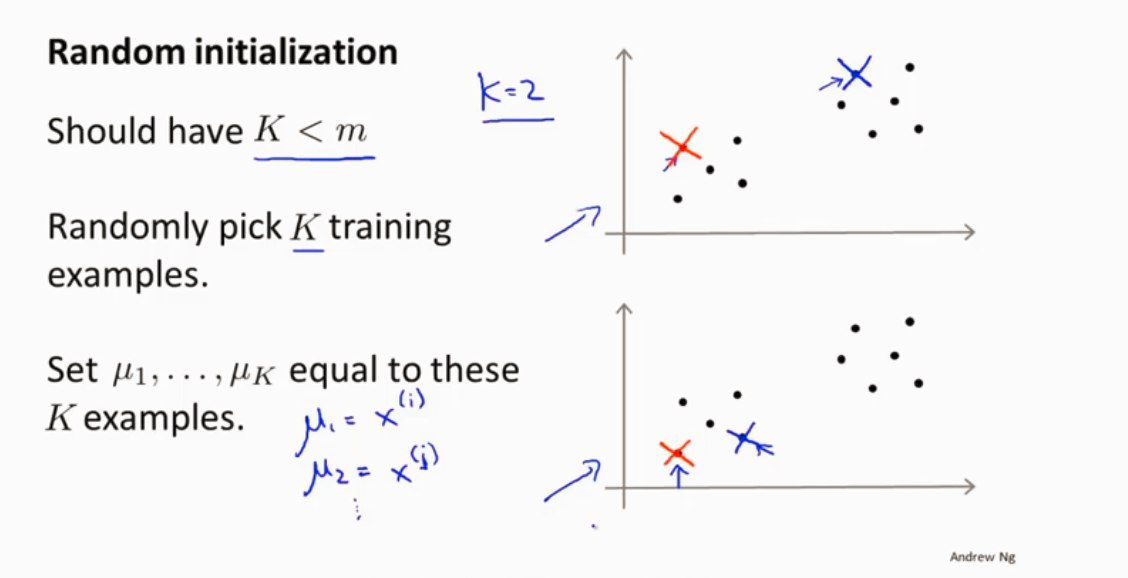
有可能局部最优
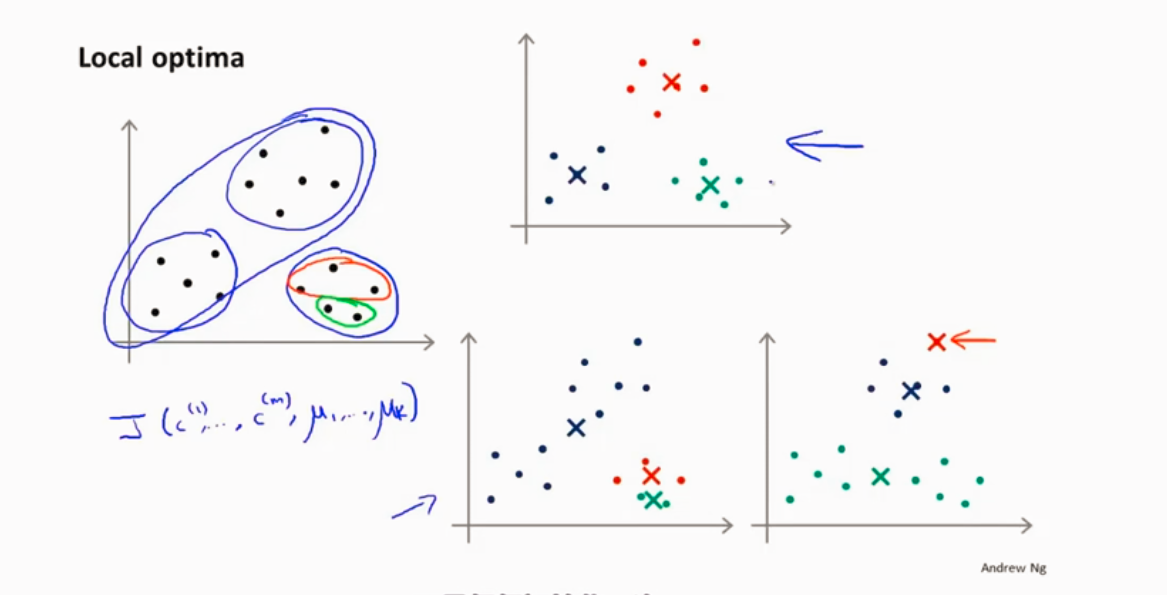
防止局部最优 可以多次随机初始化
在多次的结果中选择代价最小的那一次
k 比较小 比较适用 k 2~10 比较好

如何取选择K的值(聚类数量)
1.
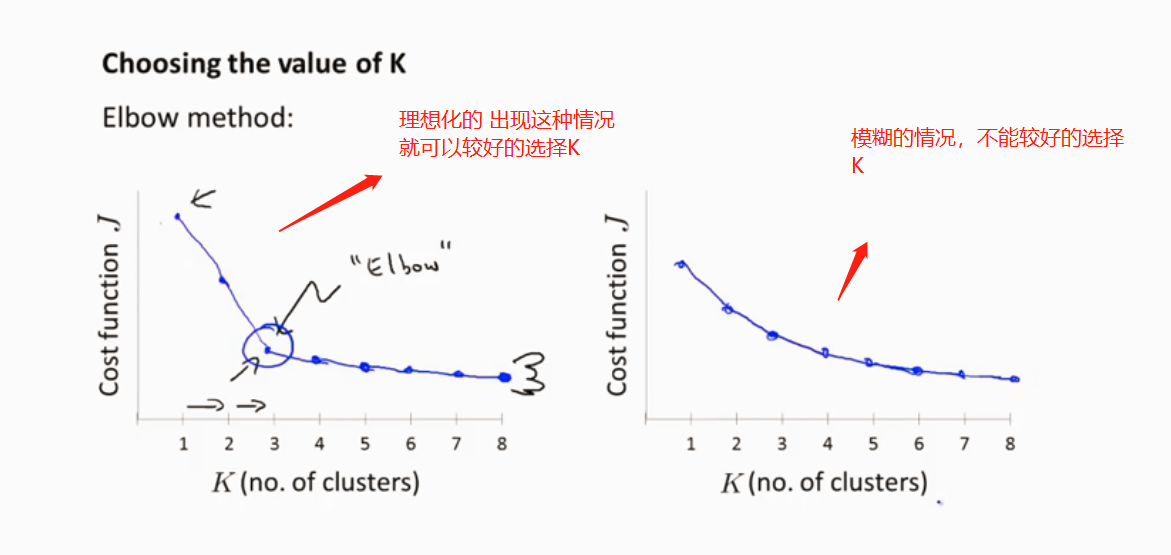
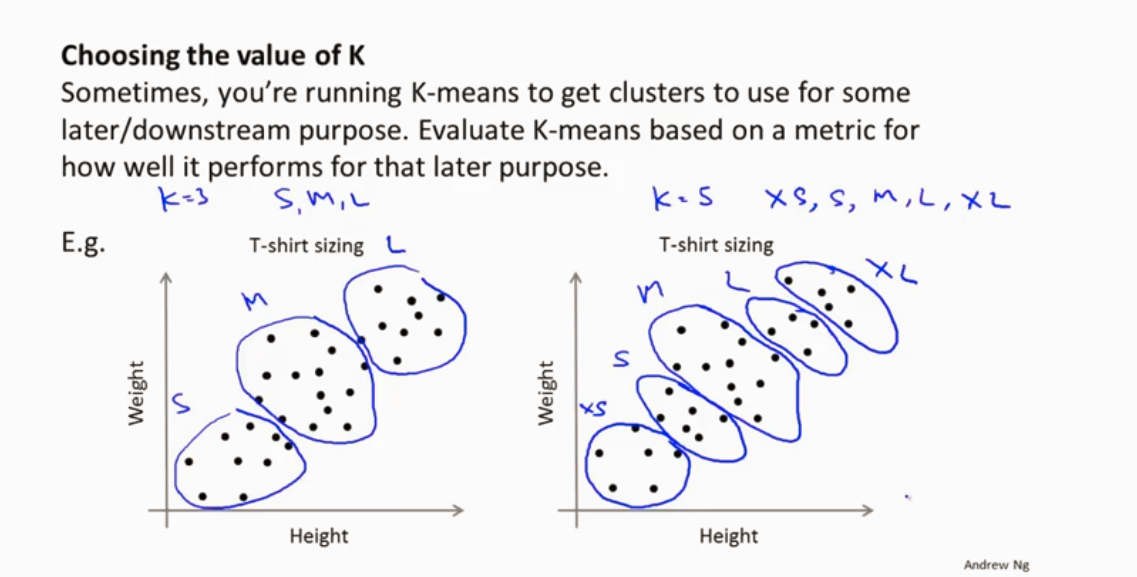
2.根据实际需求
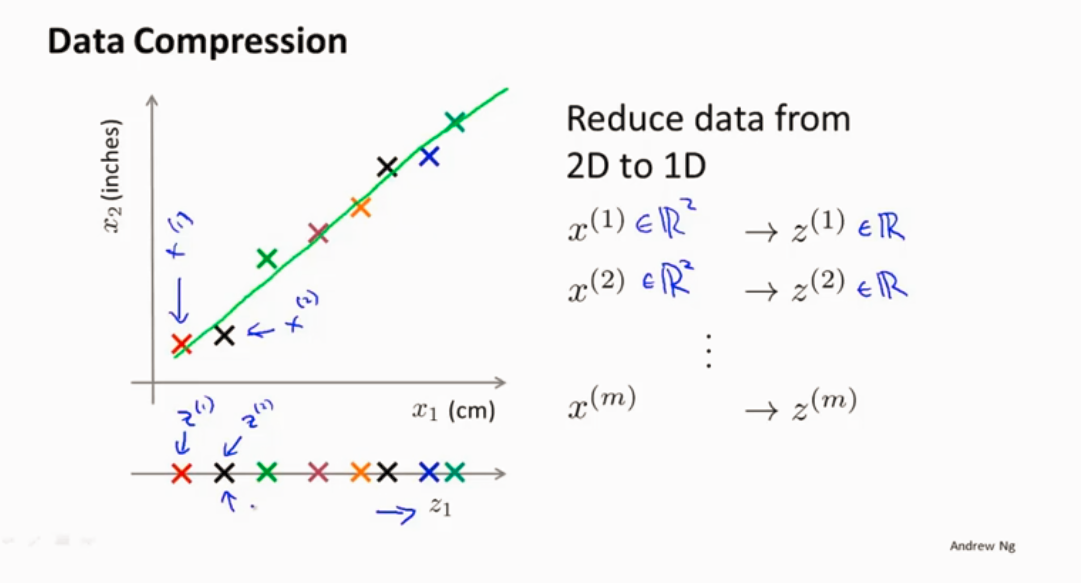
降维
作用 数据压缩
2D->1D
3D->2D
都投影到一个平面上
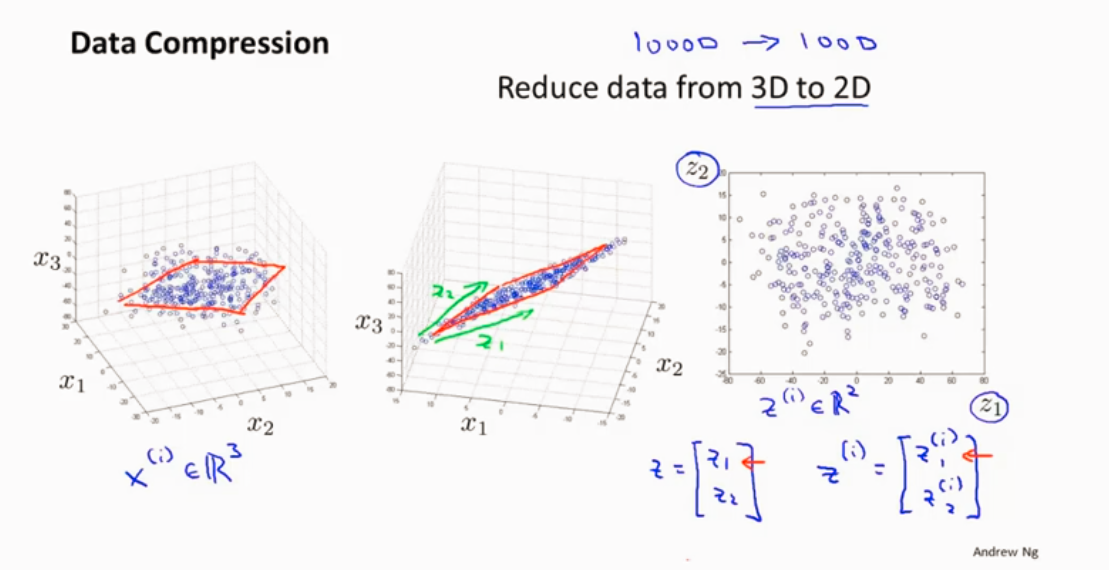
作用 可视化数据
PCA 算法
降维算法 :当前流行的算法:主成分分析方法(PCA) 最小化平方投影误差
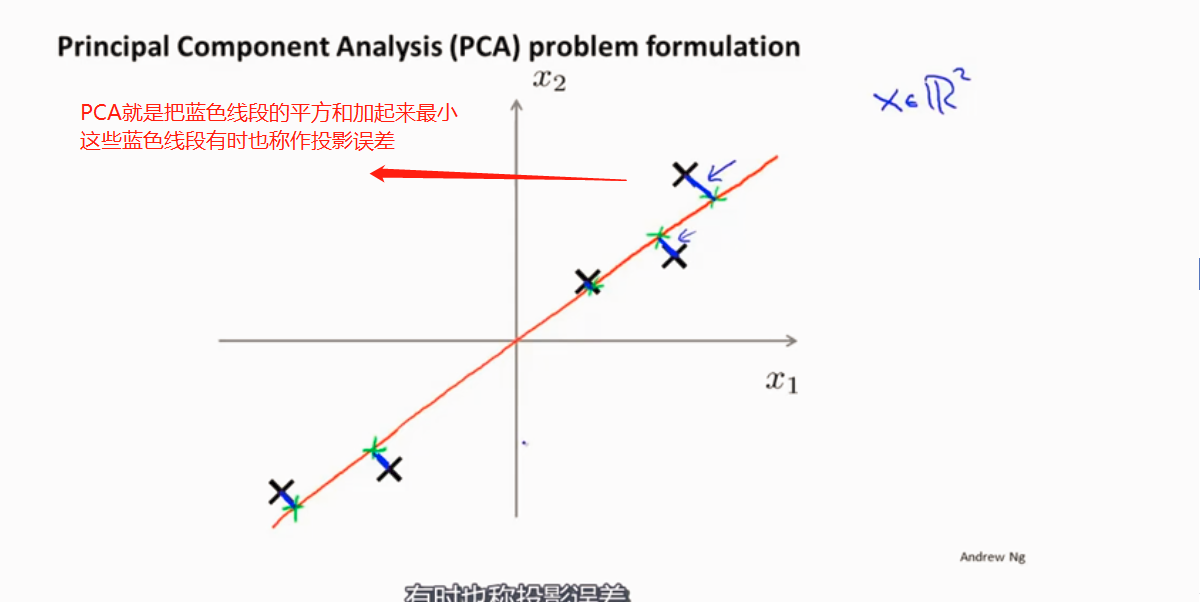
PCA将 个特征降维到 个,可以用来进行数据压缩,如果100维的向量最后可以用10维来表示,那么压缩率为90%。同样图像处理领域的KL变换使用PCA做图像压缩。但PCA 要保证降维后,还要保证数据的特性损失最小。
PCA技术的一大好处是对数据进行降维的处理。我们可以对新求出的“主元”向量的重要性进行排序,根据需要取前面最重要的部分,将后面的维数省去,可以达到降维从而简化模型或是对数据进行压缩的效果。同时最大程度的保持了原有数据的信息。
在应用PCA前,先进行均值归一化和特征规范化。
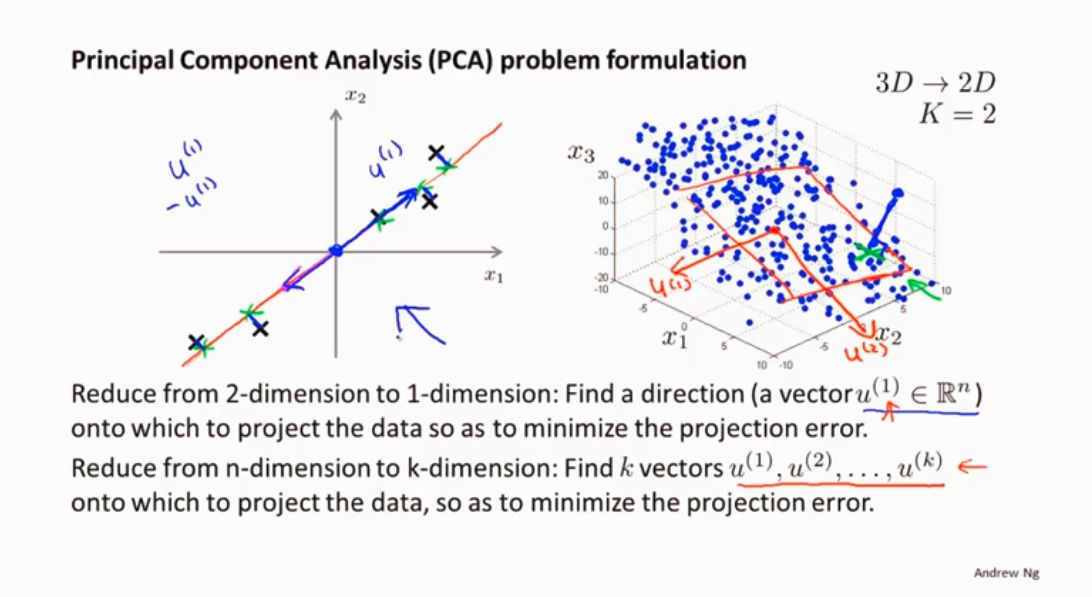
PCA和线性回归的区别
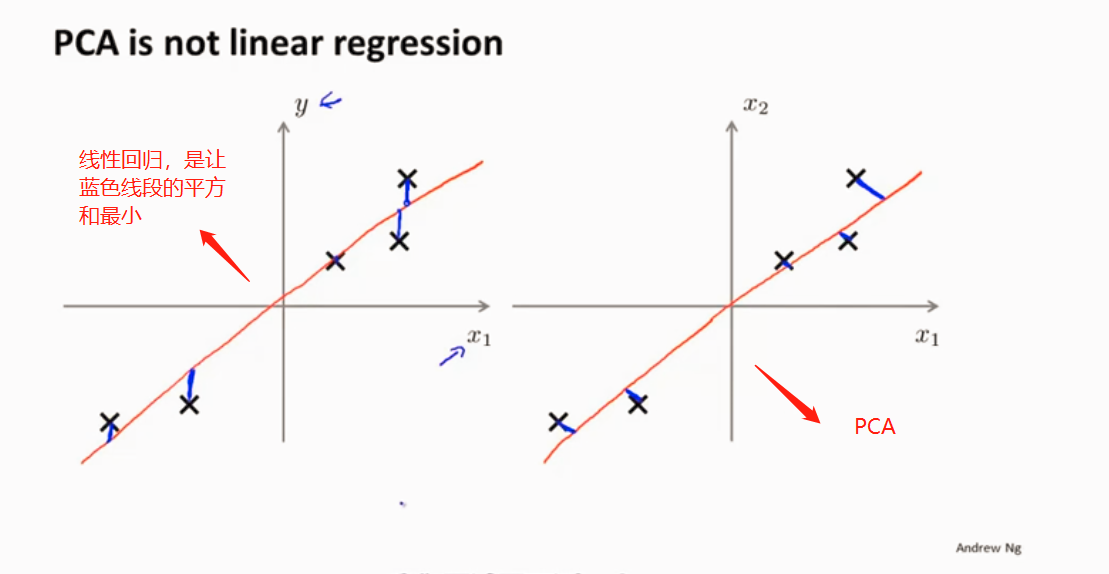
PCA之前首先数据预处理

对于数据降维后PCA如何在新的维度进行计算呢,
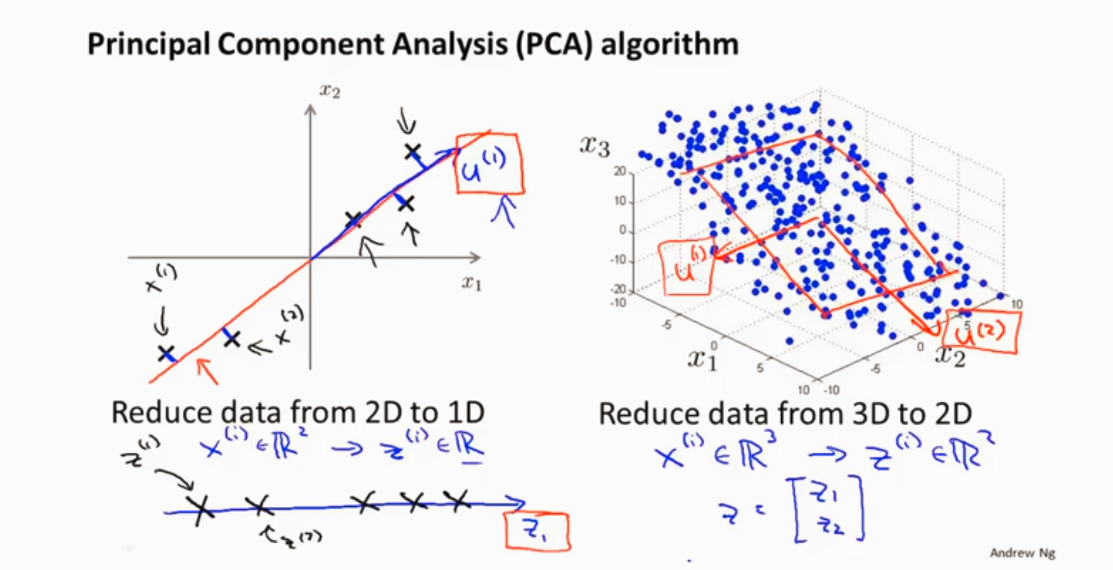

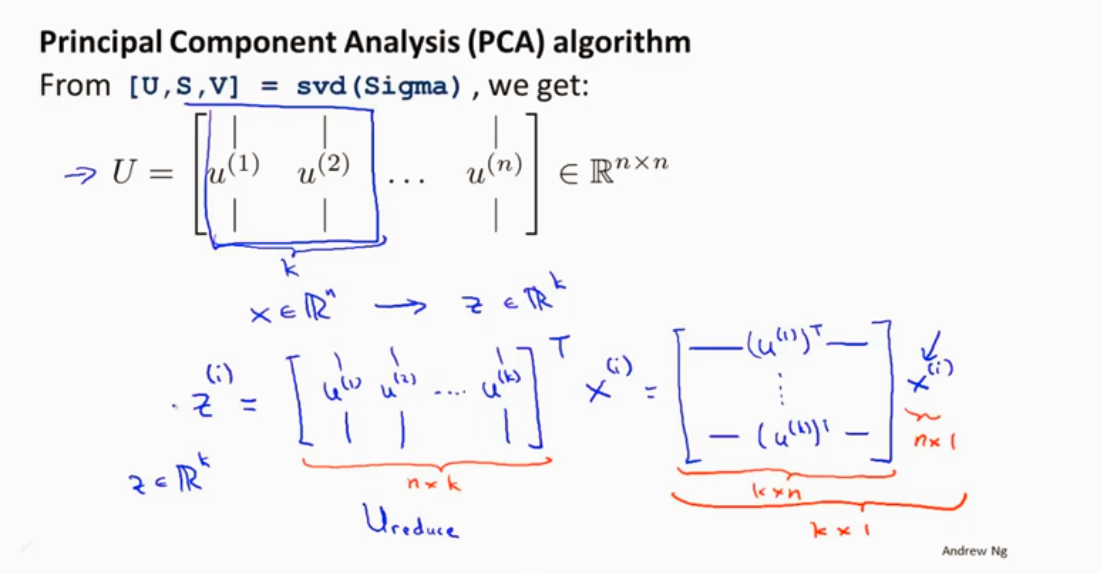
从 n 维 降到k维
k(主成分)

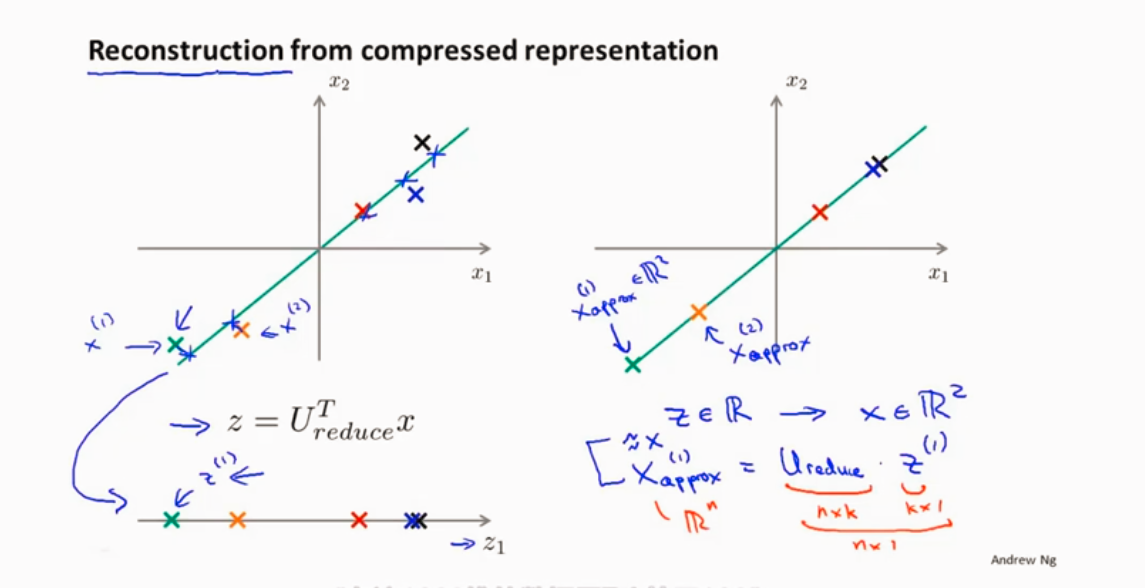
从低维回到高维
如何选择K (主成分数字)
x和其投影的平均距离除以数据的总方差 希望这个数值小于0.01

那么如何实现呢
SVD(奇异值分解)


应用PCA
应用PCA对监督学习问题加速
先用PCA将数据压缩降维 一般可以减少到1/5 或者1/10
PCA 可以减少对内存和硬盘空间的需求
PCA仅在训练集上进行,不在测试和交叉验证集上进行
定义到了X-Z的映射后,可以应用这个映射在测试和交叉验证集上


PCA不要用于防止过拟合 ,正则化是解决过拟合好的方法
PCA提高算法速度较好

异常检测
高斯分布 正态分布
异常检测算法

分离数据

异常检测算法和监督学习算法比较
异常检测算法适用于正样本少,大量负样本。
而监督学习算法则在有大量正样本下适用比较好。

特征的选择 使用log函数是特征更像高斯分布 (调整参数)
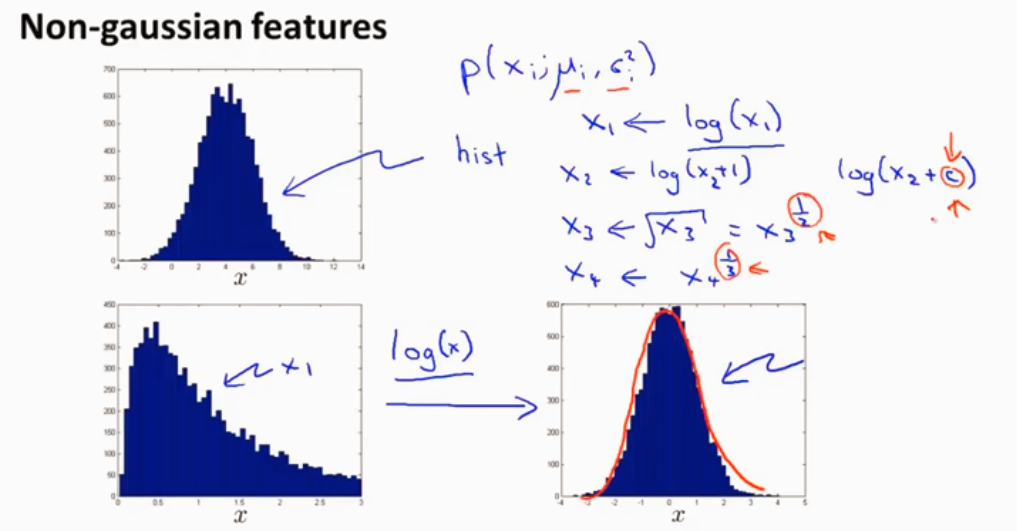
如何得到异常算法的特征 误差分析
通过没有拟合的数据(异常样本)来进行参考看看能不能改进优化
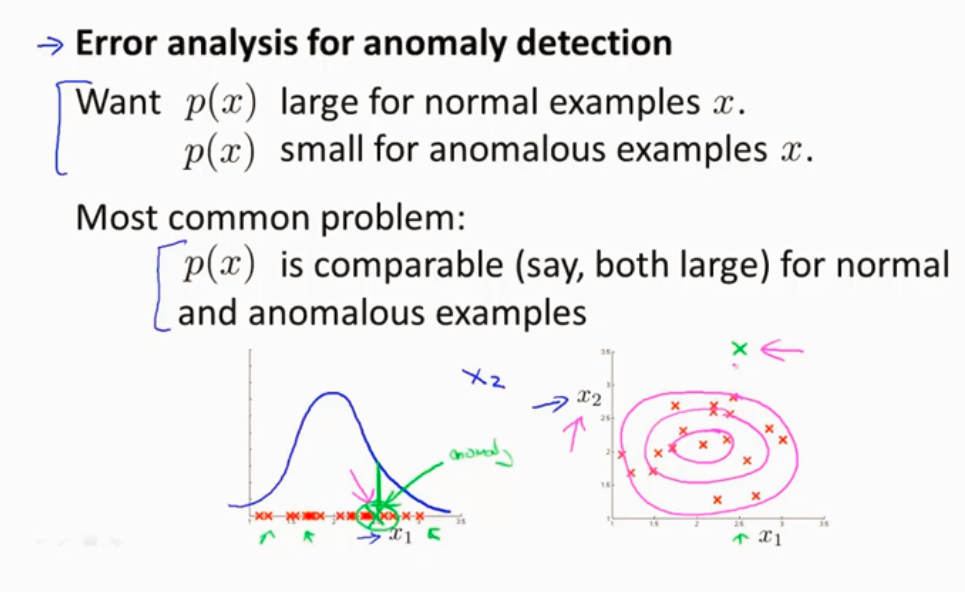
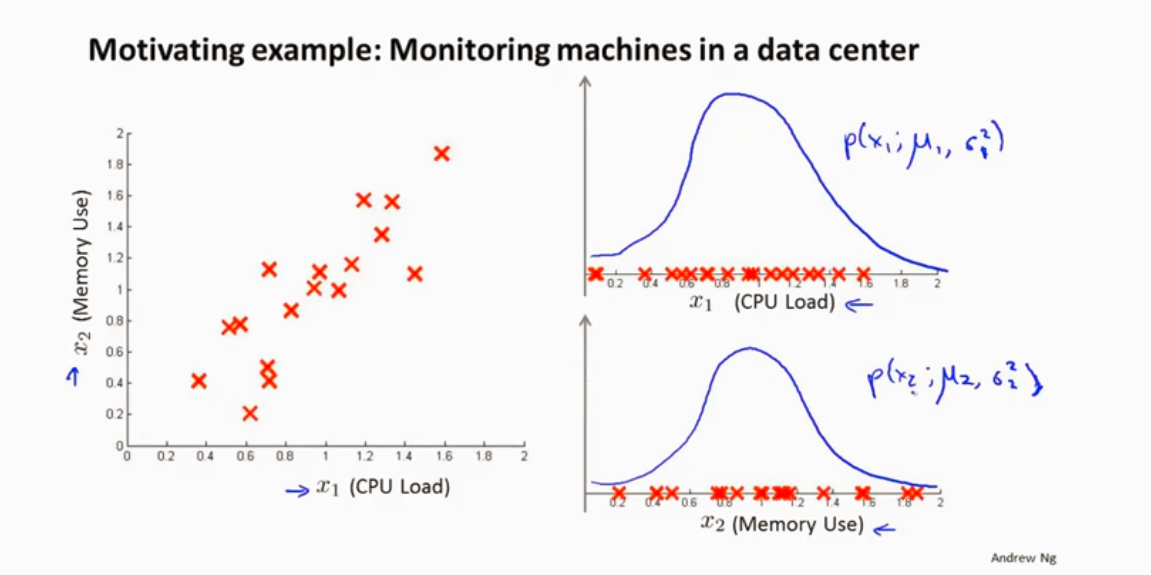
异常检测算法给数据特征建模,把X1和X2的特征单独提取出来构建高斯函数
异常检测算法的一个问题,如下图,绿色的样本是异常样本,但是异常检测算法认为它一般,是因为异常检测算法使粉色的范围,识别不出蓝色区域是好的样本,所以我们需要改进一下。
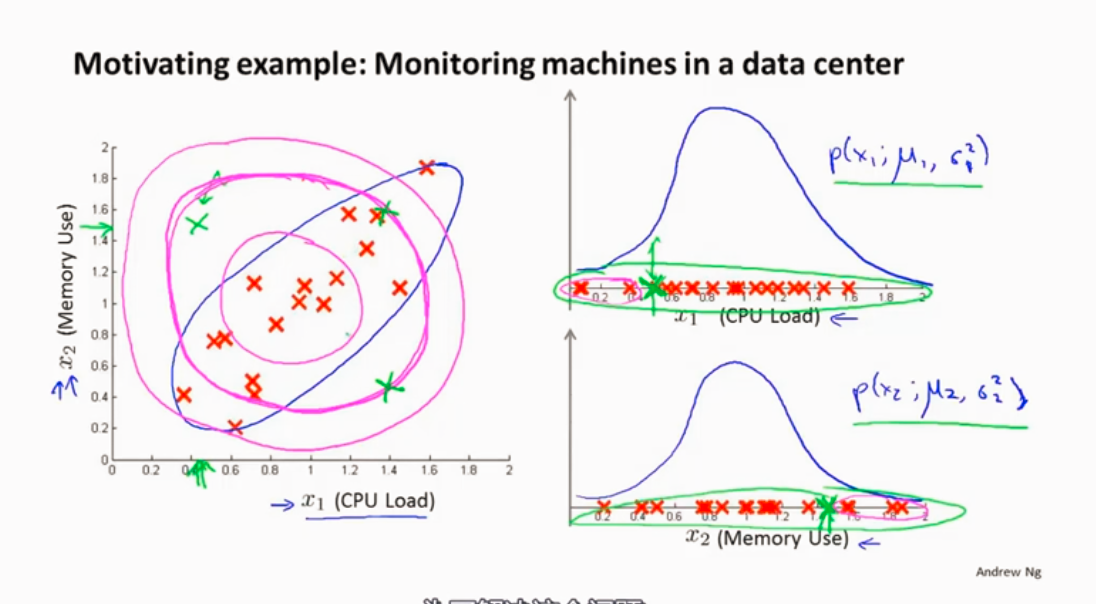
所以会用到多元高斯分布

多元高斯分布与异常检测算法结合

原始模型和高斯模型使用情况分析
特征 n很大的时候 可以用原始模型。
多元高斯模型适用的n比较小,样本的数量大于特征的数量 ,m>>n的时候应用高斯模型

推荐系统
基于内容的推荐算法
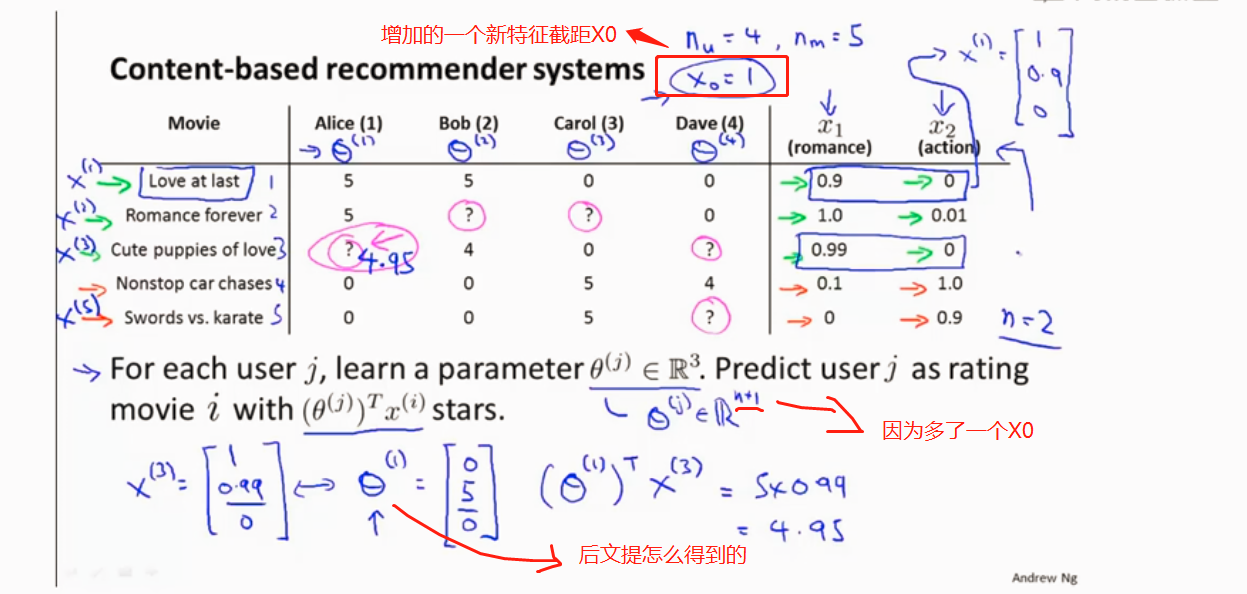
算法步骤
如何选择θ, 使训练样本的预测值减去实际值平方和最小化。是代价函数最小

求所有用户的θ


协同过滤
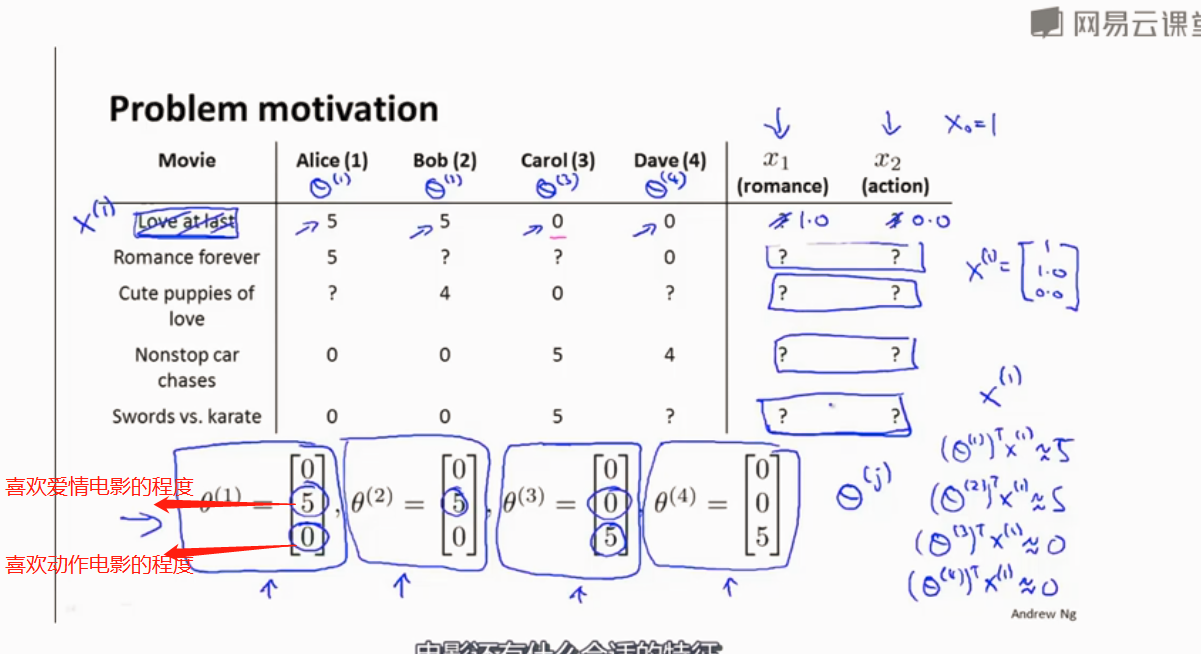

协同过滤算法
将两种结合起来,不应一直不断重复求X和θ了
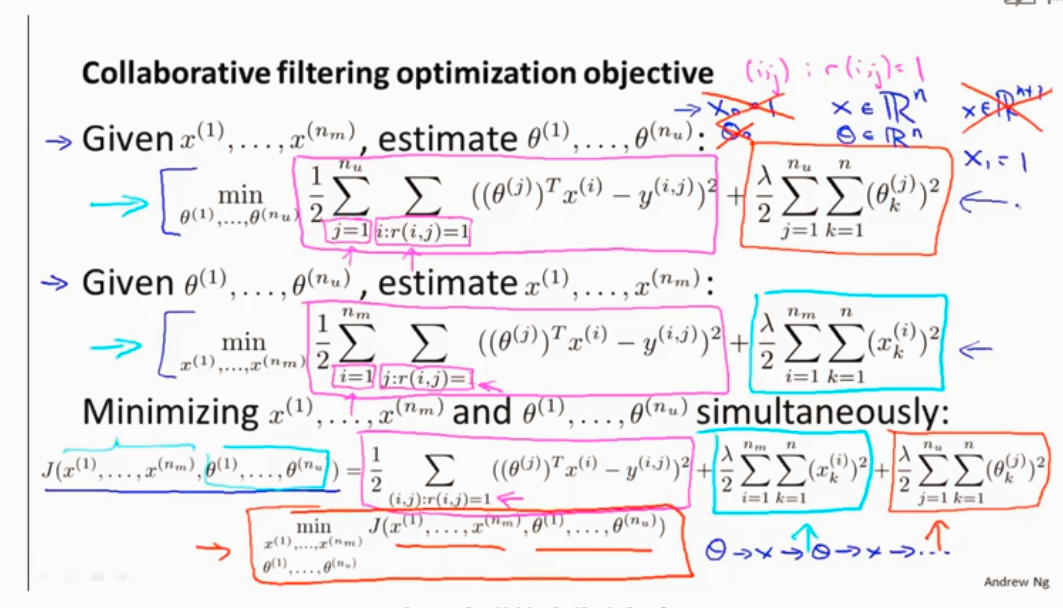
算法步骤

低秩矩阵分解(协同考虑算法矩阵向量化)

推荐相关的电影

均值归一化

计算均值

大规模机器学习 (大数据量)
数据量很大的时候,对所有样本进行梯度下降,显然是不明智的选择。
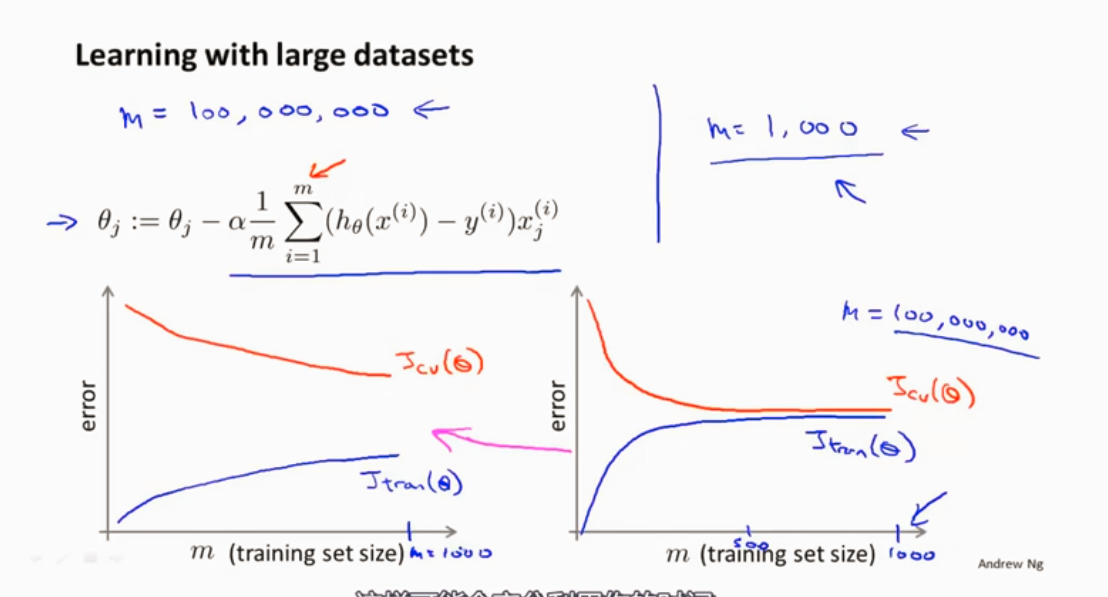
所以就应用了随机梯度下降,还有另一种叫减少映射,来处理海量的数据集。
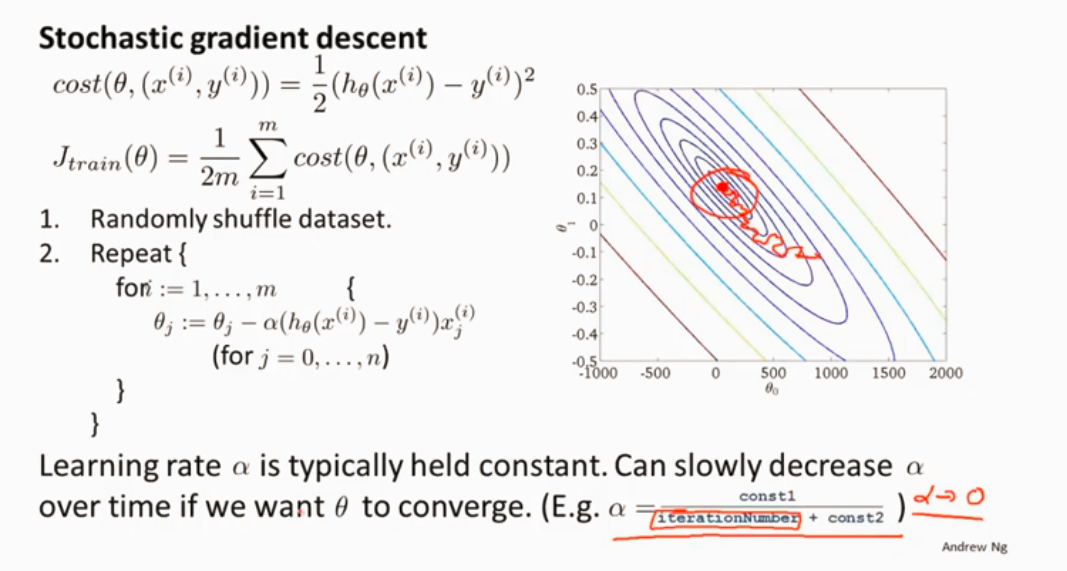
随机梯度下降
线性回归为例

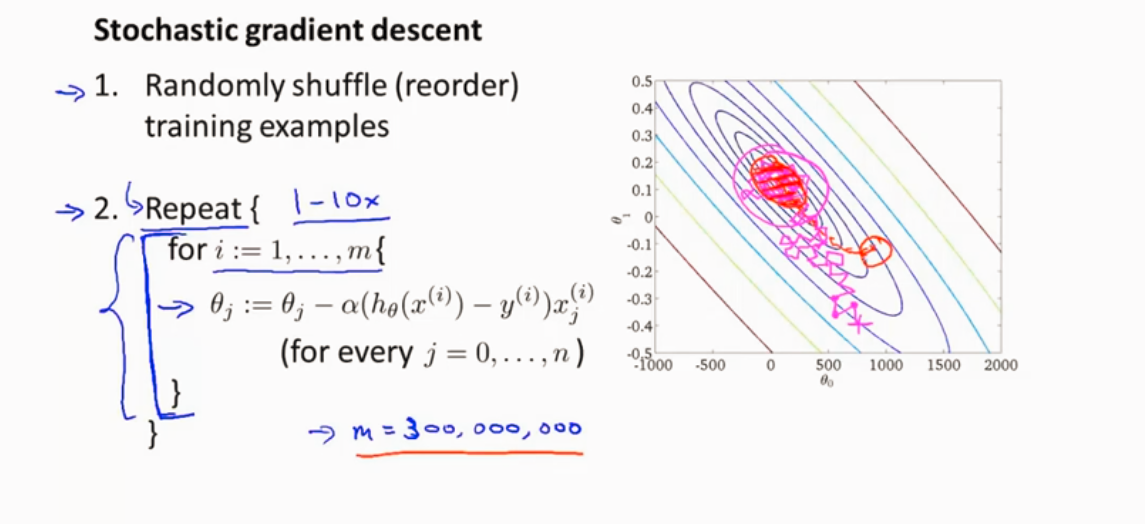
检测算法是否收敛

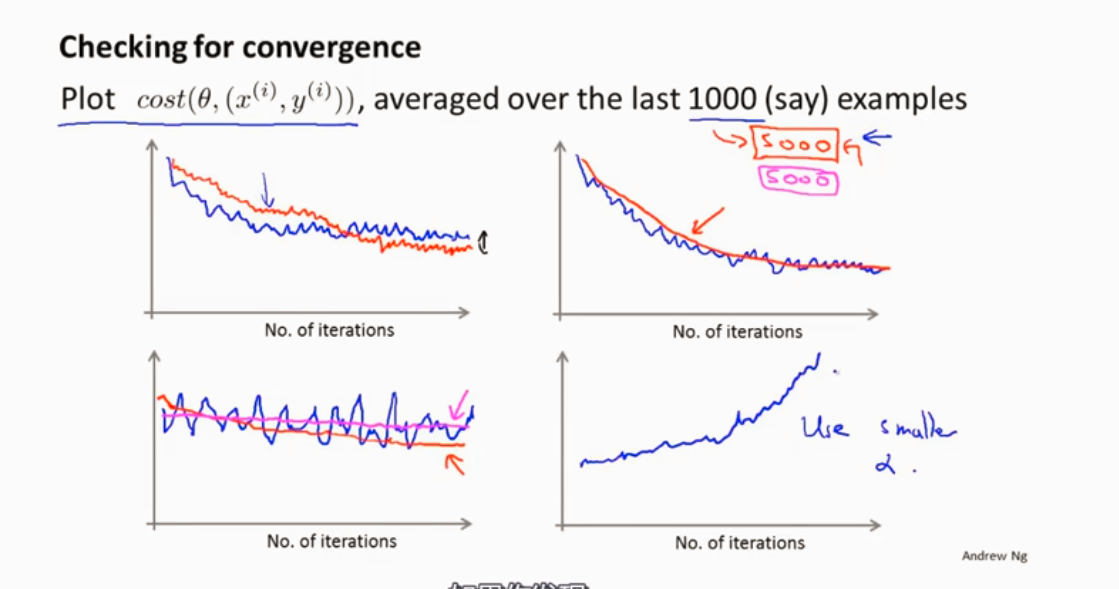
在随机梯度下降算法中,一般是让α为一个常数值,还有一少部分让α随着时间来变动(减小),使能更好的趋向全局最优。
Mini-batch梯度下降
一次选取b个样本进行计算

需要确定好b

在线学习算法
大型网站有连续的数据流,可以更好的应用在线学习算法。